HyperTreeGrid in VTK: Cursors and Supercursors
This is the fifth installment in a series of blog articles about vtkHyperTreeGrid (HTG) usage and implementation in VTK. The first part, an introduction about HTG, can be found here, the second part, HTG data construction, can be found here, the third part, HTG: Using Masks, can be found here and the fourth part, HTG: Specific Filters, can be found here.
In what follows, we will focus on different cursors and supercursors that can be used with HTG data structures.
Introduction
Citing the aforementioned articles, we can now represent and store all tree-based, rectilinear axis-aligned AMR meshes we want to support.
Operating efficiently on these data structures is a different story however. HTGs have two main properties that must be respected during traversal: depth-limitation and bit-masking. In order to respect these properties, the methods interacting with this type of data must enforce their conservation
Because a HTG is inherently a collection of hypertrees, it is only natural to iterate over these as a way to traverse it in its entirety.
To traverse a HTG, it is highly encouraged to use the following abstractions: hypertree accessor and iterator, cursor and supercursor.
Hypertree accessor and iterator
To allow direct access or iteration through the hypertrees, we introduce the hypertree accessor and the hypertree iterator in Fig. 1.
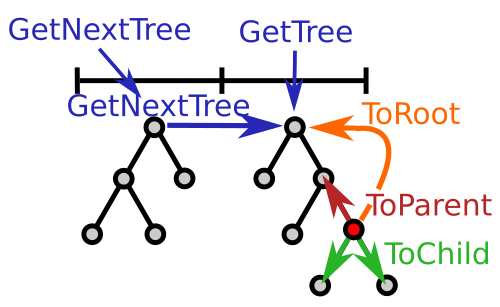
GetTree(nHT): From a defined hypertree grid, one can access directly the nHTth hypertree.
GetNextTree(): A hypertree iterator can be created from a hypertree grid, and GetNextTree() is then called to iterate through all the defined hypertrees, thus avoiding undefined hypertrees.
Cursors
Using the hypertree obtained from either hypertree accessor or iterator, it is possible to ask the HTG object to create what we call a cursor. This cursor will only operate on the hypertree it has been created on.
A cursor is a structure pointing to a vertex of a hypertree in a hypertree grid, that can both access its vertex attributes and move from its current vertex to another connected vertex.
Any cursor will hold at least the following information: a reference to the hypertree it is traversing and the local identifier of the vertex it is pointing to. From this information it is possible to retrieve the associated global indexing. Also, it is noteworthy that, by design, cursors are richer than iterators because they do not impose a predetermined traversal scheme. Displacement operators might be available in each cursor in Fig. 1.
ToChild(iChild): Descend into the vertex with child index iChild, respecting depth-limiter and bitmask, relative to the vertex currently pointed at, except if already at a leaf.
ToParent(): move one vertex up in the tree, except if already at the root.
ToRoot(): move to the root of the tree.
From these displacement operations, one can easily implement usual tree traversal such as Depth-First-Search (DFS) or BreadthFirst Search (BFS).
Fragrances
Like perfumes, concrete cursors types are created from a mixture of fragrances. Below, we define several fragrances to meet different needs and allow for efficient implementations.
Movement fragrance
The Movement fragrance (not default value), i.e. the Oriented or NonOriented values, expose the following displacement operators:
Oriented: ToChild(iChild).
NonOriented: ToChild(iChild), ToParent() and ToRoot().
- The NonOriented fragrance also has the GetLevel() method described later.
The oriented concept indicates that a progression in width or depth is a one way street and, as such, not reversible.
Geometric fragrance
The Geometric fragrance (expressed when present) allows to know the geometric properties of the cell like its coordinates, its size and eventually the level of depth.
Geometry: GetOrigin(), GetSize(), GetBounds(bounds), GetPoint(xyz), [GetLevel()]
Level fragrance
The Level fragrance (expressed when present) allows us to know the level of depth where we are.
Level: GetLevel() retrieve the current level (depth) of the cursor
This fragrance is automatically available with the Orientation fragrance if we are in a NonOriented cursor.
Unlimited fragrance
The Unlimited fragrance (expressed when present) is the ability to descend beyond a leaf cell, building a virtual representation of endless decomposition.
Unlimited: IsRealLeaf(), GetExtensivePropertyRatio()
The method IsLeaf() always returns True, unless we reach the limit fixed by the depth limiter. The method IsRealLeaf() returns True for non-virtual leaves.
The GetExtensivePropertyRatio() method returns the value of the ratio to be applied, by multiplication, to an extensive value (i.e. scaling with volume in 3D or surface in 2D) of a cell. For intensive valued fields this ratio should not be used.
Supercursors
Many visualization algorithms require neighborhood information to perform their computations. For instance, the outside boundary extraction algorithm generates a boundary face if and only if it is not shared by two cells.
A super cursor is a cursor that keeps track of a connectivity information based on the hypertree grid.
In order to provide this type of topological information we devised and implemented the following compound structures .
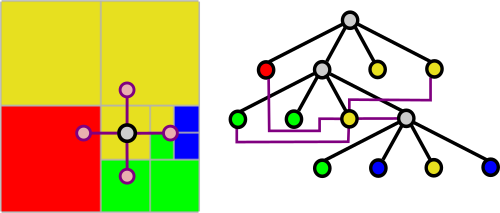
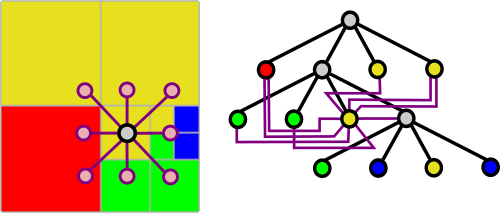
Implementing a supercursor thus entails providing the logic necessary when operating on the hypertree to up-date the neighborhood information which might be spread across several hypertrees of the hypertree grid.
When a supercursor is created, its central cursor references the cell root of the considered hypertree and neighborhood information corresponds to the different root cells of the neighbor hypertrees.
Topological fragrance
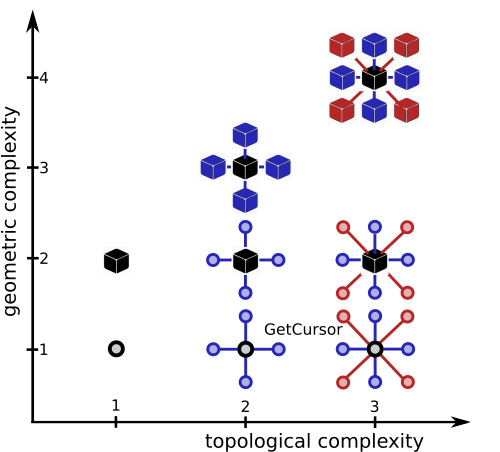
The Topological fragrance describes the topological complexity related to neighborhood information.
Cursor: No neighbors descriptions (the default when non expressed)
VonNeumannSuperCursor: Neighbors in 1−d by points, 2−d by edges, in 3−d by faces
MooreSuperCursor: Neighbors by points, edges and faces
Neighbors fragrance
This fragrance drives the presence of the geometric features in neighbors cursors.By default, super-cursors maintain all the geometric information and simple cursor none.
Light: Only the center cursor contains a Geometric fragrance (expressed when present)
See Fig 4 for a complete overview:

Remark
The computational complexity of a cursor is directly related to the fragrances assigned to it. This is evident with VonNeuman’s supercursor and severe with Moore’s supercursor (with a ~25 fold increase in complexity, although it depends a lot on the define case of the TB-AMR mesh).
| Cursor | GeometricCursor | VonNeumannSuperCursor | MooreSuperCursor | |
| AxisClip | ✓(output) | ✓ | ||
| AxisCut | ✓(output) | ✓ | ||
| AxisReflection | ||||
| CellCenters | ✓ | |||
| Contour | ✓(pre-processing) | ✓ | ||
| DepthLimiter | ||||
| EvaluateCoarse | ✓ | |||
| Geometry | ✓(d <3) | ✓(d <3) Light | ||
| Gradient | ✓ Default/Unlimited | |||
| ImageDataToHTG | ✓(output) | |||
| PlaneCutterprimaldual | ✓(pre-processing) | ✓ | ✓ | |
| PlotOverLine | ✓ | |||
| Threshold | ✓ | |||
| ToDual | ✓ | |||
| ToUnstructuredGrid | ✓ |
It is of course possible to define new fragrances.
Similarly, should other types of connectivities arise in the future, these would readily find their place along the topological complexity scale. This ability to extend the functionality of the cursors allows us to refine the algorithms to optimize execution speed.
Conclusion
Like perfumes, each proposed concrete cursor type is created from a mixture of fragrances and named by concatenating the fragrances’ terminology. Only the types of cursors that are required for our needs are currently implemented and they are as follows:
- OrientedCursor
- NonOrientedCursor
- OrientedGeometricCursor
- NonOrientedGeometricCursor
- NonOrientedVonNeumannSuperCursorLight
- NonOrientedMooreSuperCursorLight
- NonOrientedVonNeumannSuperCursor
- NonOrientedMooreSuperCursor
- NonOrientedUnlimitedMooreSuperCursor
References
This article is heavily inspired by the following unpublished article https://hal-cea.archives-ouvertes.fr/cea-03501320/document
CEA, DAM, DIF, F-91297 Arpajon, France