A Greedy Patch-based Image Inpainting Framework

We present a system for filling holes in an image by copying patches from elsewhere in the image. These patches should be a good continuation of the hole boundary into the hole. There is typically no “right answer” as we are extrapolating image data into an unknown region. For this reason, human observers giving varying levels of “it looks pretty good/realistic” responses to the output image is usually the only metric used to judge the quality of such algorithms. This implementation is intended to serve as a reference implementation of a frequently cited algorithm for patch-based inpainting, as well as to provide a framework for users to easily experiment with modifications to such methods.

Several ideas implemented in this work were taken from or inspired by the algorithm described in “Object Removal by Exemplar-Based Inpainting” by Criminisi et. al.

The latest code is available here: https://github.com/daviddoria/PatchBasedInpainting

Terminology
Concepts are too often obfuscated by complex notation, so we will refrain from using such notation as much as possible. Before proceeding, we must define some terms:

• The source region is the portion of the image that is known (is not part of the hole) at the beginning, or has been already filled.
• The target region is the hole to be filled.
• An isophote is simply an image gradient vector rotated by 90 degrees. It indicates the direction of “same-ness” rather than the direction of maximum difference, as the gradient indicates.

Demonstration
Below we show a synthetic demonstration of the algorithm. The inputs to the algorithm consist of an image and a binary mask that is the same size as the image. Non-zero pixels in the mask indicate the region of the image that is considered the hole to inpaint/complete/fill. In this example, the image consists of a black region (top) and a gray region (bottom).  This simple example is used for testing because we know the result to expect – the dividing line between the black region and gray region should continue smoothly.

 Figure 1 (a) Image to be filled. The region to be filled is shown in bright green. (b) The mask of the region to inpaint. (c) The result of the inpainting.

In real images, the result will never be  good. The next image we show is an example of completing a real image. This result shows the typical quality of inpainting that the algorithm produces.

Figure 2 (a) Image to be filled. The region to be filled is shown in bright green. (b) The mask of the region to inpaint. (c) The result of the inpainting. This took about 30 seconds on a P4 3GHz processor with a 206×308 image and a patch radius = 5.

Algorithm Overview
The algorithm reads an image and a binary mask. Non-zero pixels in the mask indicate there is a hole to fill. Set the size of the patches that will be copied. Determining a good patch size is a very experimental process. Once a patch size is decided, locate all the patches of the image that are completely inside the image and entirely in the source region.

Take note that the main loop does the following:

• Computes the priority of every pixel on the hole boundary.
• Determines the boundary pixel with the highest priority. We will call this the target pixel. The region centered at the target pixel and the size of the patches is called the target patch.
• Determines which source patch to copy into the target patch.
• Copies the corresponding portion of the source patch into the target region of the target patch.
• Updates the mask/hole to reflect the copied patch.
• Determines which image patches are newly fully valid and adds them to the list of source patches.
• Repeats until the target region consists of zero pixels.

Algorithm Details
Two parts of the algorithm deserve much discussion:

1. How do we choose which boundary pixel has the highest priority?
2. How do we decide which source patch to copy into a specified target patch?

Priority Computation
Since these patch-based methods are greedy (there are a few attempts at globally optimal, patch-based solutions including “Image Completion Using Efficient Belief Propagation via Priority Scheduling and Dynamic Pruning” by Komodakis), selecting a good order in which to fill the hole is very important. We provide several priority computation classes that work up Criminisi’s method. The base class, Priority, has a simple interface so users can implement their own priority functions for experimentation.

Random Priority
This class simply returns a random pixel on the hole boundary. This is fast, but likely not a very good choice.

Onion-Peel Priority
Filling in pieces near the edge of the hole should intuitively be easier than filling in pieces deep within the hole. This class encapsulates the idea that the outside of the hole should be preferred over boundary pixels that are now deep inside of the original hole. This technique gets its name because with a regularly shaped hole, the algorithm will chew away at the entire outside of the hole before moving further inside, an order that resembles peeling an onion. To enforce this behavior, a confidence image is maintained. Initially, the confidence outside of the whole is 1 (very sure) and the confidence inside of the hole is 0 (totally unsure). You can think of confidence as a measure of the amount of reliable information surrounding the pixel. In Criminisi’s method, the confidence of a pixel is defined as:

When a patch is filled, Criminisi updates all pixels in the hole region of the target patch in the confidence image with the confidence value of the target pixel.

Criminisi Priority
Criminisi noted that continuing/filling linear structures first is very important in making the result look believable. Therefore, a data term is computed as:

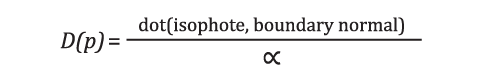
This function encourages first filling target pixels that have strong isophotes in a similar direction to the hole boundary normal.

The priority P(p) of a pixel p is then given by the product:

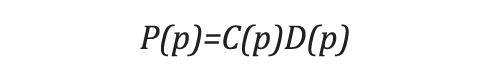
Alpha is a normalization factor that should be set to 255 for grayscale images, but that value also seems to work well for RGB images. In fact, in Criminisi’s priority term, alpha is a scalar multiple of a term that is only used once minimized; the value of alpha is actually irrelevant. No initialization is necessary to compute this priority term because it is not recursive. That is, it can be computed from the image+hole information directly at each iteration.

Choosing the Best Source Patch
Once a target pixel is selected, we must find the “best” source patch to copy to its location. Criminisi proposed comparison of a source and target patch by computing the normalized sum of squared differences between every pixel that is in the source region of the target patch and the corresponding pixels in each source patch.

Implementation Details
There is a caveat that should be noted in the computation of the isophotes. We originally tried to compute the isophotes using the following procedure:

• Convert the RGB image to a grayscale image.
• Blur the grayscale image.
• Compute the gradient using itkGradientImageFilter.
• Rotate the resulting vectors by 90 degrees.
• Keep only the values in the source region.

The figure below shows the gradient magnitude with and without the modification, which we will explain.

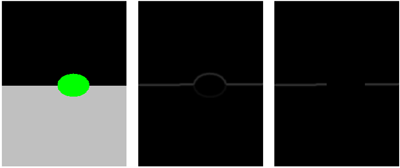
 Figure 3 (a) The image to be filled. The target region is shown in green. (b) The naively computed gradient magnitude. (c) The
gradient magnitude of the image with the slightly expaned hole.

The high values of the gradient magnitude surrounding the target region are very troublesome. The resulting gradient magnitude image using this technique is sensitive to the choice of the pixel values in the target region, which we actually want to be a completely arbitrary choice (as it is unknown, it should not affect anything). More importantly, the gradient plays a large part in the computation of the pixel priorities, and this computation is greatly disturbed by these erroneous values. Simply ignoring these boundary isophotes is not an option because the isophotes on the boundary are exactly the ones that are used in the computation of the Data term. To fix this problem, we have discovered two solutions.

Immediately dilate the mask specified by the user. This allows us to compute the isophotes as described above (naively), but now we have image information on both sides of the hole boundary, leading to a valid gradient everywhere we need it to be. The only drawback to this approach is that we have made the problem a bit harder by making the hole slightly bigger.

As an alternative solution, use a non-patch based technique to coarsely fill the hole (e.g. Poisson editing/hole filling – see the following Source article). This solution is very blurry deep inside of a large hole, but is reasonable at the hole boundary. This procedure produces values inside the boundary of the hole that when used in a gradient computation yield a gradient image that is very close to what we would expect.

Code Snippet
The PatchBasedInpainting class must be instantiated using the type of image to be inpainted. Then the patch radius must be set, the image and mask provided, and the Inpaint() function called.

inpainting.SetPatchRadius(5);
inpainting.SetImage(image);
inpainting.SetMask(mask);
inpainting.Initialize();
inpainting.Inpaint();
ImageType::Pointer result =
  inpainting.GetCurrentOutputImage();

A full demonstration is provided in the file: PatchBasedInpaintingNonInteractive.cpp.

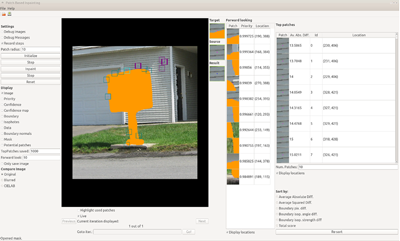
GUI
Debugging an algorithm like this can be very hard. Even when things are working correctly, inspecting each step can lead to valuable insights. We have created a Qt GUI to enable this type of inspection. Its features include:

• All of the important images can be toggled on/off including the image, the mask, the boundary, and the priority.
• The inpainting can be advanced automatically or one step at a time.
• The top N matching source patches at each iteration are displayed in a table along with the scores.
• The locations of the target patch and top N source patches can be overlayed on the image.

A screenshot of the GUI is shown below:

Conclusion
In this article we described a common algorithm for filling image holes in a patch-based fashion. We also provided and detailed an implementation of such an algorithm that is written in such a way to hopefully promote future experimentation and research in this area.

David Doria is a Ph.D. student in Electrical Engineering at RPI. He received his B.S. in EE in 2007 and his MS in EE in 2008, both from RPI. David is currently working on hole filling in LiDAR data. He is passionate about reducing the barrier of entry into image and 3D data processing. Visit http://daviddoria.com  to find out more or email him at daviddoria@gmail.com.