Fast deformation dynamics using model order reduction in iMSTK

Introduction

In iMSTK finite element method is often the method of choice to simulate soft tissue mechanics. Depending on the geometric complexity of the anatomical model, the degree of freedom can quickly grow leading to a high computational burden which can have adverse effects on the frame rate and interactivity. Parallelization (see our recent blog), strategies such as adaptive time-stepping and graded mesh can alleviate some of the computational burden but sometimes, depending on the scenario, one may run out of cost-cutting options. A reduced-order model for the deformation dynamics was introduced to iMSTK to address this issue.

Model order reduction (MOR), also called dimensional model reduction, provides quantitatively accurate descriptions of the dynamics of a system at a computational cost that is much lower than the original numerical model. The idea is to project the original, high-dimensional solution space onto a low-dimensional subspace to arrive at a reduced model that approximates the original system. The low-dimensional subspace is carefully chosen such that the most important characteristics (often known as modes) of the original system’s behaviors are preserved. With much fewer degrees of freedom, the reduced model can be solved much faster than the original system. It has been extensively used in many disciplines, including fluid dynamics, mechanics, computational biology, circuit design, and control theory. MOR is often used in the computational mechanics community for large scale simulations [4] and offers an excellent opportunity for low-cost deformable tissue models.

Deformation dynamics with MOR

A finite element (FE) modeling of the partial differential equations of elasticity on a discretized spatial domain produces ordinary differential equation (ODE) of the form $latex Mu+Du + f_{int}(u) = f_{ext}$ where $latex u$ is the displacement field, $latex M, D, R^{3n \times 3n}$ ($latex n$ is the number of nodes) are the mass and damping matrices, respectively and $latex f,f_{int} \in R^{3n}$ are the internal and external forces, respectively. MOR produces a low-dimensional subspace of size $latex r ( \ll 3n)$ spanned by the columns of $latex U \in R^{3n \times r}$ allowing us to approximate the solution $latex u=Uz$ where $latex z \in R^r$ is the reduced coordinates. Similarly, the above-mentioned ODE can be posed and solved in the reduced space. The obvious advantage is that $latex r \ll 3n$ is much less than $latex n$ resulting is a much faster solution to the reduced ODE after which the full-space solution can be recovered from $latex u=Uz$.

Barbič et al. [1] showed that for geometrically non-linear material models that are commonly used to model deformation in iMSTK, the internal force can be approximated as a cubic polynomial in $latex z$ whose coefficients can be precomputed and stored at a cost of $latex O(r^4)$. Using numerical quadrature rules, the precomputation cost can be further reduced to $latex O(r^2)$[2]. The subspace basis U is time-invariant, mass-orthogonal ($latex U^TMU=I$), and depends on geometry, boundary conditions, and material properties. A good subspace consists of the low-frequency modes that correspond to the least resistant deformations. The basis can be constructed using linear modes and their modal derivatives, which span the natural second-order system response for large deformations. With k linear modes, users can choose a fraction of $latex k(k+1)/2$ modal derivatives available. One of the advantages of this approach is that no a priori knowledge of runtime interaction is required and therefore the precomputation needs to be performed only once. The full details of the above-described procedures can be found in [1].

MOR in iMSTK

iMSTK uses Vega [3] as a backend for FE-based deformation dynamics. Recently, we have exposed MOR features of the Vega library (see release 3.0) that implements the above-described approach. iMSTK’s dynamical models implement dynamically evolving models that have the ability to simulate 3D elastic continua, fluids, elastic membranes, and 1D structures. A new dynamical model ReducedStVK was introduced that solves the reduced model for deformation. The following code snippet shows how to create and configure the dynamical model with pre-computed coefficients of the cubic polynomials (.cub file) for the reduced internal forces, and the other the basis matrix (.float file).

auto dynaModel = std::make_shared<ReducedStVK>();

auto config = std::make_shared<ReducedStVKConfig>();
config->m_cubicPolynomialFilename = iMSTK_DATA_ROOT "/heart.cub";
config->m_modesFileName = iMSTK_DATA_ROOT "/heart.float";

dynaModel->configure(config);

Results

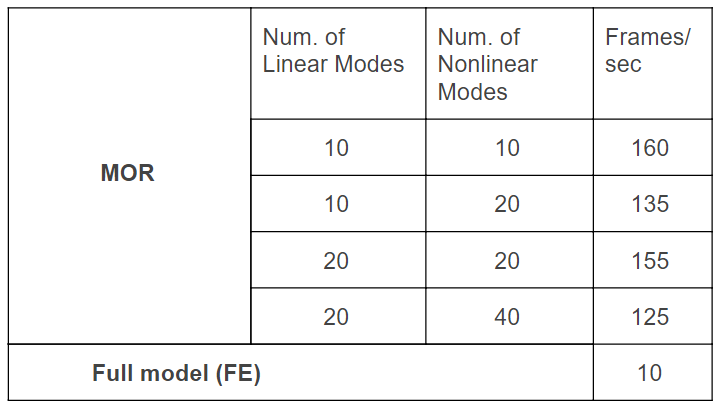
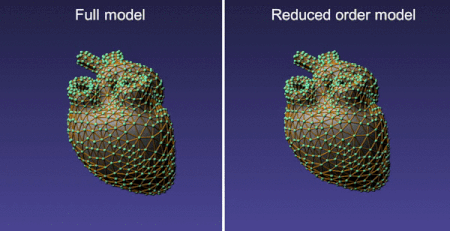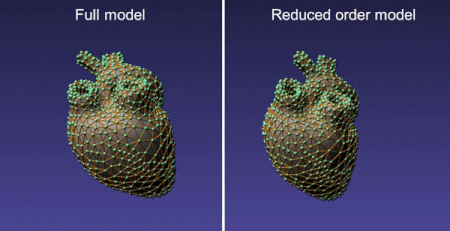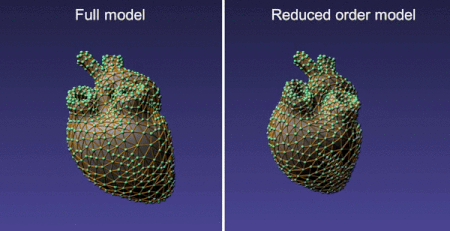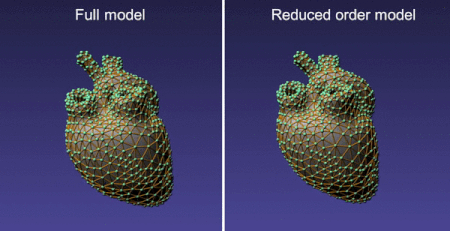
The table above compares the speed of MOR that uses a different number of linear and non-linear basis with the traditional FE dynamical model for a tetrahedral mesh with 12827 elements (and 12K degree of freedom). As can be seen, MOR is 12-16 times faster than traditional FE based dynamical models for this case. Furthermore, we have observed that with only 20 non-linear modes, the results from MOR agree quite well (visually) with that using FEM.

Discussion

The reduced model employs a dense matrix solver (whereas the full model results in a sparse system) and hence further optimizations are possible (eg. using MKL). The reduced basis depends on the boundary conditions, material constants, and mesh topology. Therefore, MOR can only be employed for simulations that do not change these at runtime.

Acknowledgements

This work was supported, in part, by the following awards from NIH: R44DE027595, 1R01EB025247, 2R44DK115332. R44AR075481 (Disclaimer: The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH and its institutes.)

References

[1] J. Barbič. Real-time Reduced Large-Deformation Models and Distributed Contact for Computer Graphics and Haptics. PhD thesis, Carnegie Mellon University, Aug. 2007.

[2] S. S. An, T. Kim, and D. L. James. Optimizing cubature for efficient integration of subspace deformations. ACM Trans. on Graphics, 27(5):165:1–165:10, 2008.

[3] Sin, F.S., Schroeder, D. and Barbič, J. (2013), Vega: Non‐Linear FEM Deformable Object Simulator. Computer Graphics Forum, 32: 36-48.

[4] Vorst, H. A. v. d., Schilders, W. H., Rommes, J. (2008). Model Order Reduction: Theory, Research Aspects and Applications. Germany: Springer Berlin Heidelberg.