Octree-based Collision Detection in iMSTK

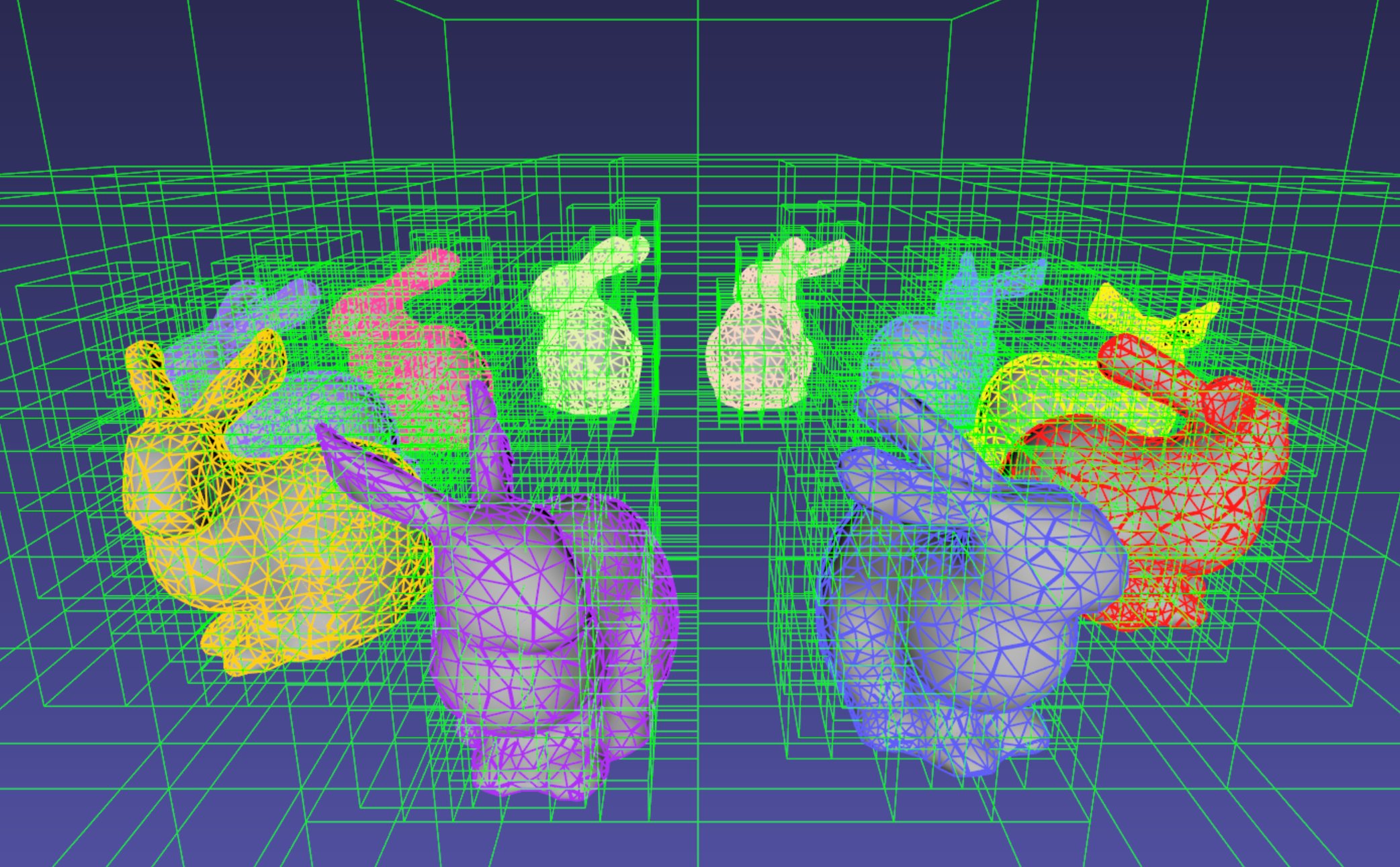
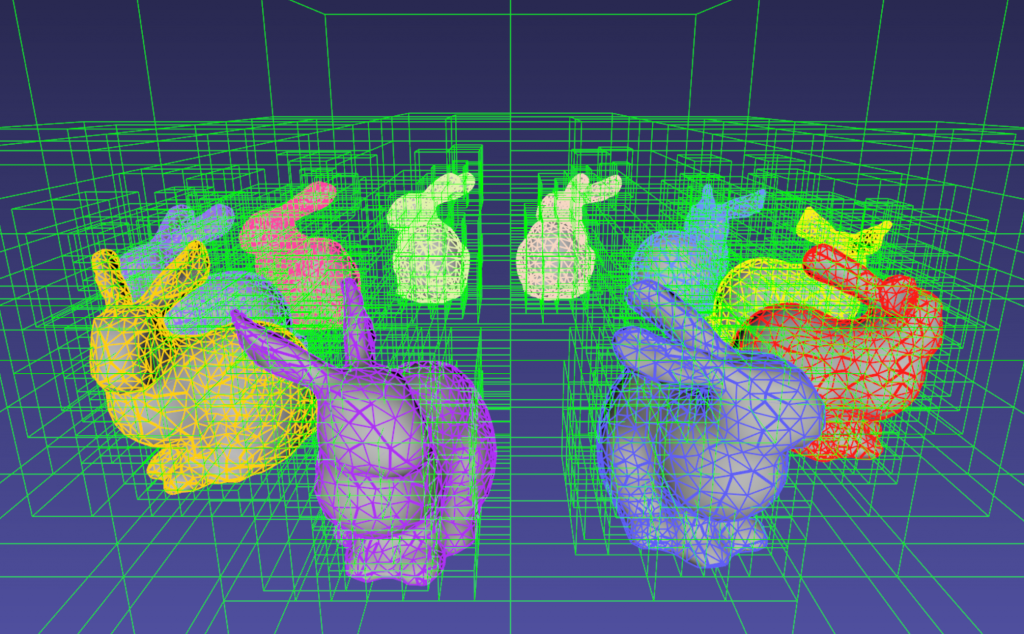
Introduction

iMSTK is an open-source toolkit written in C++ that helps to rapidly prototype interactive multi-modal surgical trainers and planners. A typical simulation scenario can feature multiple objects interacting with each other in real-time. Collision detection is the first step to resolving the physical contact between the objects that are typically represented using a collection of simpler geometric primitives such as vertices, edges, and triangles. Collision detection algorithms are tasked to not only detect and but also report the geometric details of all the points of contact. Accurately and efficiently detecting collisions between interacting objects and handling them using appropriate mechanisms can enhance the accuracy and the realism of application.

Collision detection is typically divided into two phases: (a) the broad phase where a set of candidate collision primitive pairs is identified, and (b) the narrow phase where the geometric intersection tests are performed on these candidate primitive pairs [1]. The narrow phase intersection tests are computationally expensive and hence the broad phase algorithms aim to achieve smallest possible candidate set of collision pairs (with all the actual collision pairs being a subset) with a minimal computational cost.

The broad phase algorithms typically employ hierarchical spatial partitioning data structures such as octrees or BVH to organize and store geometric information for efficient retrieval and processing. Collision detection has been researched extensively in the computer graphics area and its implementation can vary widely depending on the assumptions that are valid for the problem at hand and the target hardware. We have chosen to implement octree-based collision detection in iMSTK. Octree data structure presents many advantages notably allowing a good balance between the cost for updating and searching for candidates primitives pairs for collision, and its suitability for parallel execution which is typically expected for real-time simulation applications.

Octree-based collision detection

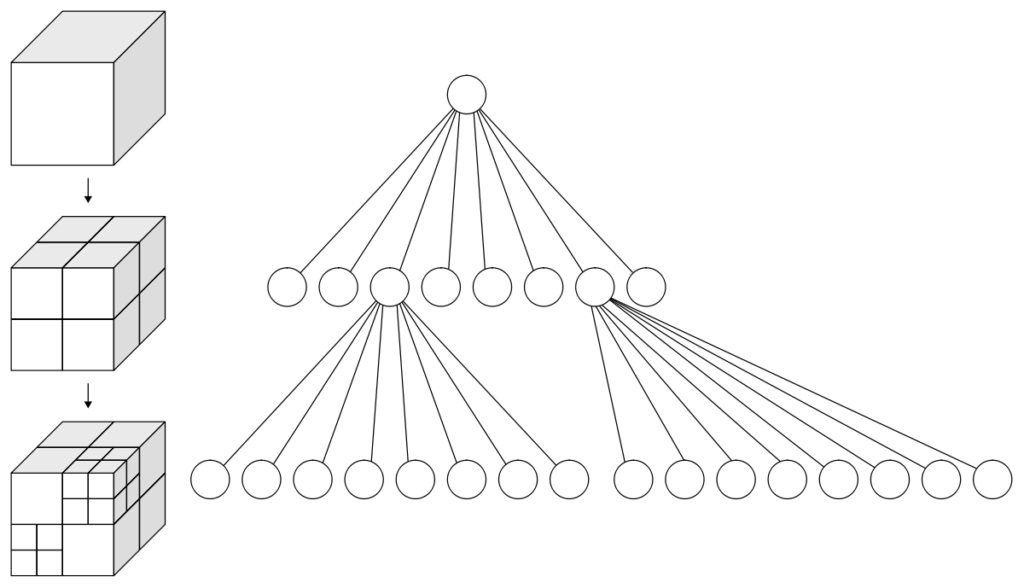
An octree is an axis-aligned hierarchical data structure that is generated by recursively subdividing the axis-aligned bounding box (AABB) into eight equally-sized cells as necessary (Figure 2). Generally speaking, the choice of whether to subdivide an octree node or not depends on the density of information present at that node which in this case is the geometry of the primitives.

Broad Phase

A brute-force way to find collisions between a set of n disjointed primitives can mean testing all the possible pairs which can be computationally prohibitive requiring O(n²) work. The broad phase of the collision detection aims to efficiently eliminate a subset of primitive pairs (also called culling) that are guaranteed not to collide thus leaving only fewer combinations for which expensive geometric tests are performed. An efficient broad phase algorithm aims to minimize the size of the left out pairs while still retaining guarantees (i.e., all the colliding pairs are part of this set).

The broad phase of the octree collision detection consists of two stages:

• Tree update: In this step, each primitive under consideration for collision are assigned to an octree node depending on the spatial extent, position, and orientation. For this purpose, the AABB of each primitive is recursively checked against the cells starting at the root node. A primitive will be assigned to a node if either the primitive size exceeds the extent of the cells of the child nodes or the current node cannot be further subdivided due to a preset limit on the maximum depth of the octree. 
• Culling: This step aims to take advantage of the spatial partitioning of the octree and eliminate as many non-colliding primitive pairs as possible from the list of all the possible pairs. Given a primitive, it is first checked for intersection with the boundary of the root node. If the primitive does not intersect with the node boundary, no further operation is performed with the tree node. Otherwise, it is then tested for intersection with all the primitives stored in the tree node. This process is then recursively called on the child nodes until reaching leaf nodes. With n primitives, detecting a collision between them has a time complexity O(nhk) in the worst case, where h is the height of the octree, and k is the maximum number of primitives at any octree node. In practice, h is around 10 and most primitives are stored at the leaf nodes; thus, the cost of detecting collision for each primitive is bounded and can be very cheap.

Narrow Phase

The broad phase outputs a set of primitive pairs that are potentially colliding and may still contain pairs that do not intersect. Therefore, in this phase, we perform intersection tests between primitive pairs, triangles in our case, that will either result in triangle-vertex or edge-edge collision data as shown in Figure 3. The triangle-triangle intersection test consists of 6 pairs of edge-triangle intersection tests as described in [1]. Other primitive types such as sphere or cube are similarly tested for intersection directly using their geometric properties.

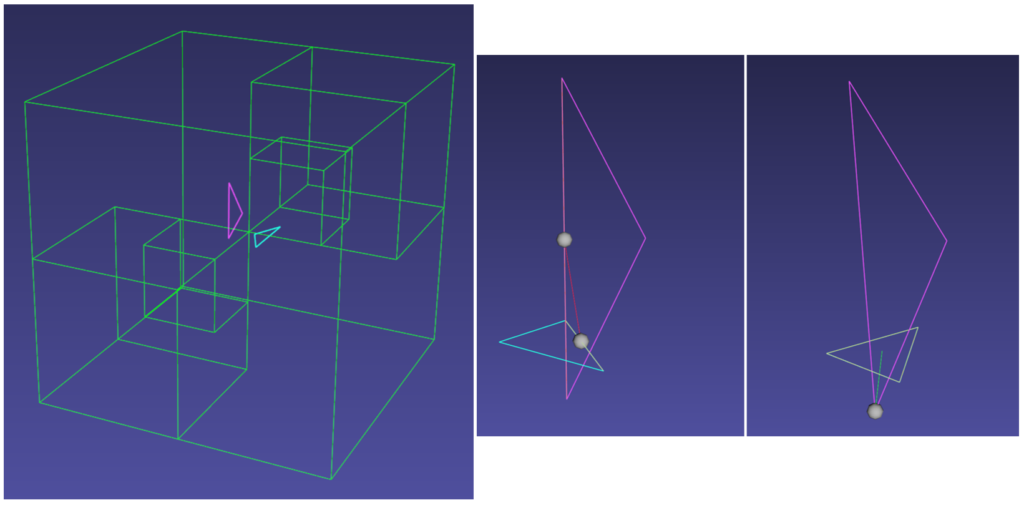
Efficiency Considerations

Loose Octree: The basic octree implementation has a significant limitation. A primitive must be kept at a node if it is not entirely contained in any of the children nodes. This can lead to situations where a very large number of primitives accumulate at a given node. As a result, the distribution of primitives may be imbalanced. This can reduce culling efficiency during the broad phase. Loose octree is a solution to this problem [1, 3] where in addition to the exact, non-overlapping boundary, each tree node has a loose boundary which is twice the size and is concentric to the actual boundary. Upon insertion, the primitives are checked for enclosure using the loose boundary instead of the exact boundary as in the basic octree implementation. Since the loose boundary is two times larger than the original boundary, the primitives are distributed evenly leading to improved efficiency. The octree in iMSTK is implemented based on this approach.

Memory management: It is evident from above that memory is allocated and deallocated frequently at each frame during the tree update step. Therefore, for efficiency considerations, we use a memory pool that recycles the allocated memory and rations new memory as needed. The memory pool is implemented as a linked list of connected memory blocks, in which each block stores eight tree nodes and a pointer to the next block. Whenever a leaf node splits, it requests a memory block from the memory pool then performs placement new to call node constructors on the given memory block. If the memory pool is exhausted, 64 blocks of memory are allocated. Discarded nodes will release their memory block back to the memory pool for reuse.

The video above shows a sample scenario consisting of 11K triangle primitives. An octree grid updated at each frame is visualized in green while the collisions are visualized using spheres between the intersecting primitives (see Figure 3). At every frame, the average time for updating the octree was less than 1ms and 10ms for computing collisions in our current implementation. These numbers render the implementation suitable for real-time, interactive simulation applications.

Usage

In iMSTK, OctreeBasedCD class embeds the implementation of the above-described functionality. Users can both access the list of primitives at any given node in the hierarchy and collision data through public API. The code snippet below shows how an octree is built and used to detect collision between two mesh objects that contain triangle primitives:

// Initialize the octree
OctreeBasedCD octreeCD(Vec3d(0, 0, 0), // Center of the root node
                       100.0, // Side length of the root node
                       0.1);  // Minimum allowed width for any octree cell

// Add mesh objects containing triangle primitives to the octree
octreeCD.addTriangleMesh(triMesh_1);
octreeCD.addTriangleMesh(triMesh_2);

// Build the Octree
octreeCD.build();

// Add collision pairs between meshes
octreeCD.addCollisionPair(triMesh_1, triMesh_2, 
                        CollisionDetection::Type::SurfaceMeshToSurfaceMesh);

At any given frame during the simulation, querying the generated collision data:

// Update octree (primitives might have moved in the prior frame)
octreeCD.update();

// Access the collision data for the mesh pair
const auto& colData = octreeCD.getCollisionPairData(
                           indx1,  // Global index of triMesh_1
                           indx2); // Global index of triMesh_2

Future Work

Octree-based collision detection operates with minimal assumptions about the connectivity or relative motion among primitives and hence is suitable for most scenarios including deformable body simulation. In the case of simulation scenarios that include rigid objects, signed distance field (SDF) and especially adaptively sampled signed distance field (ADF) [2] can achieve better performance. This is very beneficial in cases where the rigid body is a very large mesh consisting of millions of triangles. Octree-based ADF will be the direction of our future work for iMSTK.

References

1. Christer Ericson. Real-Time Collision Detection. CRC Press, Inc., Boca Raton, FL, USA, 2004.
2. Teschner, M., Kimmerle, S., Heidelberger, B., Zachmann, G., Raghupathi, L., Fuhrmann, A., Cani, M., Faure, F., Magnenat‐Thalmann, N., Strasser, W. and Volino, P. (2005), Collision Detection for Deformable Objects. Computer Graphics Forum, 24: 61-81.
3. Thatcher Ulrich. Loose Octrees. Game Programming Gems, volume 1, chapter 4.11, pages 444–453. Charles River Media, 2000.