A new VTK selection algorithm based on digital topology

Background

This blog entry continues the series of articles reporting on the results of our ongoing collaboration with Commissariat à l’Energie Atomique (CEA), Direction des Applications Militaires Île-de-France (DIF), France, where a domain-specific visualization tool based on VTK and a ParaView server is developed. In particular, in this article, we explained how we added a new selection algorithm based on a geometric criterion, namely whether cells are intersected or not by a user-specified broken line.

We now report on a novel selection algorithm, this time based on a topological criterion, which we added to VTK 6 as part of this CEA/Kitware collaboration.

Digital topology

Digital topology is a part of combinatorial topology which focuses on the neighborhood relation within a grid structure; specifically in the context of interest to us, by grid we understand a conforming mesh in 2D or 3D. This is a slight extension of the term to the the standard definition of grid cell topology, which by definition studies the case of n-dimensional topological cubes, i.e., quadrilaterals in 2D and hexahedra in 3D. In our case, however, we accept hybrid meshes, i.e., meshes containing different types of elements (e.g., triangles and/or quadrangles in 2D, hexahedra and/or pyramids, tetrahedra, wedges and knives in 3D).

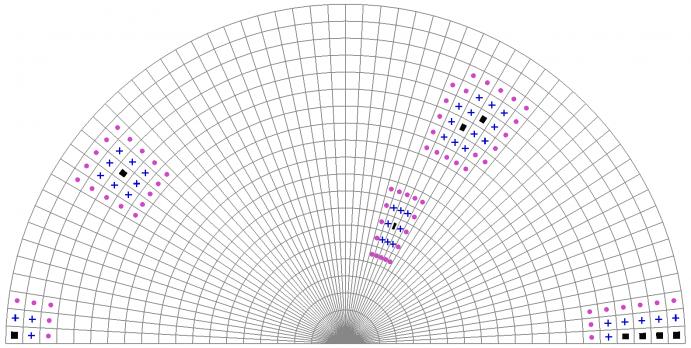
It is beyond the scope of this short article to provide a full exposition of grid cell topology. It will instead suffice to gain an intuitive understanding thereof, by knowing that it is based for the rest of this article on the notions of 8-adjacency in 2D and 26-adjacency in 3D: two distinct grid cells are said to be separated by a distance of 1 if and only if they share at least one topological entity (vertex, edge, or face). The digital distance between 2 grid cells is henceforth defined by counting the smallest number of successive such adjacencies needed to reach one cell from another one. The example below illustrates this intuitive definition, which is sufficient for our purpose of defining selection based on cell distance within a mesh.

The figure above shows a hybrid mesh (containing both triangles and quadrilaterals) together with a number of “seed” cells, marked with black glyphs. Those cells that lie at distance 1, in the sense of 8-adjacency, from any of these seed cells (excluding the latter when at distance 1 from another seed) are marked with a blue cross. The same is done for a distance of 2, with violet disk markings. This illustrates the notion of topology generated by 8-adjacency distance, which can readily be extended in the 3-dimensional case, with the 26-adjacency distance.

Cell distance selector

A class for the selection of cells at a given 8- or 26-adjacency distance D from a given set of seed cells, within a composite data set, had been developed at CEA/DIF. In the context of this current collaboration, we developed a new subclass of vtkSelectionAlgorithm, called vtkCellDistanceSelector, in order to port this functionality to VTK 6.x. We preserved almost all of the original API, except for the choice of input ports, which we modified as follows to comply with typical VTK usage:

• Input port 0: the input mesh, in the form of a vtkCompositeDataSet. In practice the permitted leaf block types are vtkPolyData, vtkStructuredGrid, and vtkUnstructuredGrid.
• Input port 1: the input set of seed cells, in the form of a vtkSelection instance atop the above.

This change therefore does not preserve backwards compatibility for the CEA/DIF visualization application, but we mitigated this by providing input port connection convenience methods, making the indexing of ports transparent to the user. With these, it will thus be straightforward to modify the aforementioned application so that it will set the inputs correctly.

In addition, we modified the original method by allowing for the inclusion or exclusion of cells located at an intermediate digital distance between 0 and D, so a topological ball rather than a disk might be selected. This is done by the means of the AddIntermediate instance variable, which by default is set to 1. Note that the implementation already allowed for the inclusion or exclusion of the seed cells themselves, with the IncludeSeed instance variable which is also set to 1 by default.

Results in 2D

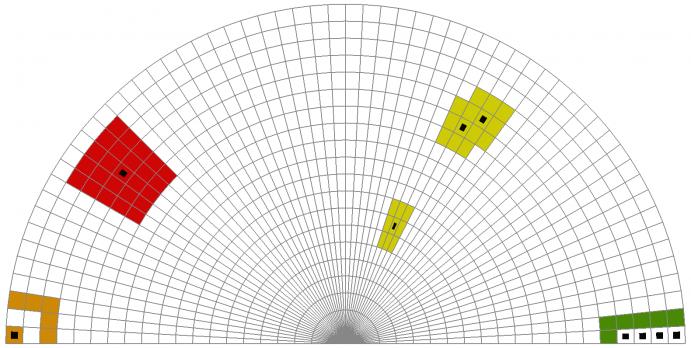
We illustrate the method first with a set of 2D test cases, which allow for convenient representation of grid cell topology relationships within a mesh. For this purpose, we make use of the same mesh and seed cells as in the example above, from which we define 4 test cases by grouping the seed cells in 4 sets: isolated interior cell, corner cell, set of 4 ridge cells, and set of 3 interior cells, 2 of which are neighbors and the third is isolated.

The picture above shows these 4 sets of seed cells. The following 4 selections are then performed with the cell distance selector:

• Red: the disk with radius 2, centered at a unique seed cell deep within the interior of the mesh.
• Green: the layer of all cells at distance 1 (exactly) of the set of 4 contiguous ridge seed cells.
• Orange:  the layer of all cells at distance 0 or 2 (but not 1) of a set of the isolated corner seed cell.
• Yellow: the set comprising all cells within distance at most 1 from the set of 3 non-contiguous seed cells.

The picture also shows the resulting sub-meshes extracted by the vtkExtractSelection filter from the output of vtkCellDistanceSelector for each of these 4 selections, using the same color encoding. Here we can readily see how this topological selection mechanism facilitates the extraction of sub-regions of interest with an intuitive and fast method of interaction.

These 4 test cases are used for non-regression testing, by the means of the TestCellDistanceSelector2D test program distributed with VTK 6.

Results in 3D

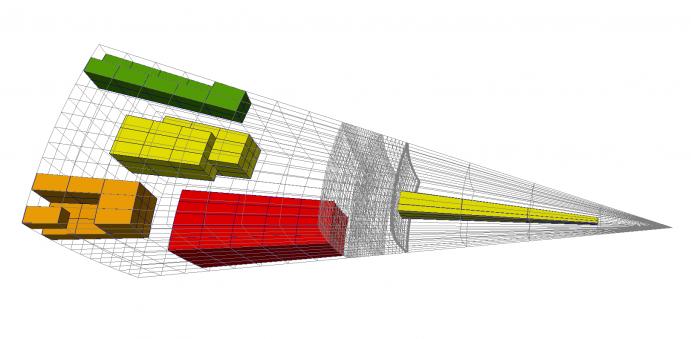
The test cases above are now extrapolated in 3D, with identical seed sell settings (isolated, connected, or non-connected sets thereof), together with the same distance requirements: equal to 1, up to 2, exactly equal to 0 or 1, or up to 1.  The figure below illustrates these selections when applied to a 3D mesh.

Specifically, the figure above shows a wireframe (light grey) representation of a 3D mesh, along with the following extracted selections, where the distance is now taken in the 26-adjacency sense:

• Red: the ball with radius 2, centered at a unique seed cell deep within the interior of the mesh.
• Green: the layer of all cells at distance 1 (exactly) of a set of 4 contiguous seed cells along a mesh ridge.
• Orange:  the layer of all cells at distance 0 or 2 (but not 1) of a set of a unique corner seed cell.
• Yellow: the set comprising all cells within distance at most 1 from a set of 3 non-contiguous seed cells.

These 4 test cases are also used for non-regression testing, by the means of the TestCellDistanceSelector3D test program distributed with VTK 6.

Conclusion and future work

A new, topology-based selection mechanism was added to VTK. This continues the expansion of the capabilities of VTK in terms of mesh manipulation and data analysis. Several continuation tasks can already be considered and proposed:

• Similarly to what had been done for the linear selector, it would be useful to have a widget allowing for convenient seed cell selection within a mesh. Coupled with the cell distance selector, such a widget would allow for interactive extraction of subsets of interest within a mesh, in the vicinity or at a given distance of cells that are know to be of particular interest (e.g., corresponding to particular conditions within a simulation or with respect to the topology of the mesh).
• Another useful addition would be to allow for different types of grid cell topologies; in addition to the current topologies based on 8- and 26-adjacency, in 2D and 3D respectively, the range of selection possibilities would be drastically improved by the addition of the topologies based on 4- and 6-adjacency.
• Finally, it would be convenient to add other distance specification mechanisms, so that an arbitrary list of distances (akin to a binary mask) could be passed as input parameters to the selection algorithm. This would make the cell distance selector one step closer to a generic, topology-based sub-mesh extraction tool.

Acknowledgments

This work was made possible thanks to a contract with CEA, Direction des Applications Militaires Île-de-France (DIF), Bruyères-le-Châtel, 91297 Arpajon, France. We extend special thanks to Guénolé Harel, Thierry Carrard, and Claire Guilbaud, for this fruitful collaboration. We are looking forward to continued collaboration with CEA/DIF in this and other areas of scientific visualization.