How the Digital Signal Processing plugin solves the temporal analysis problem in ParaView

December 14, 2023

Mathieu Westphal, Thomas Galland, Charles Gueunet, Sonia Ayme and Francois Mazen

In the first version of the DSP plugin, presented in this blog post, the main limitation is scalability and distributed computing support. In the more recent version (available in Paraview 5.12 onwards), this limitation was fully addressed and all the features were presented. Please read these previous blog before reading this one.
Let’s take some time to break down how this limitation was overcome and what makes it possible in the DSP data model.
Let’s also evaluate the performance of the DSP plugin with a public, reproducible benchmark.

Designing a data model for temporal analysis

Original design for the DSP plugin data model:

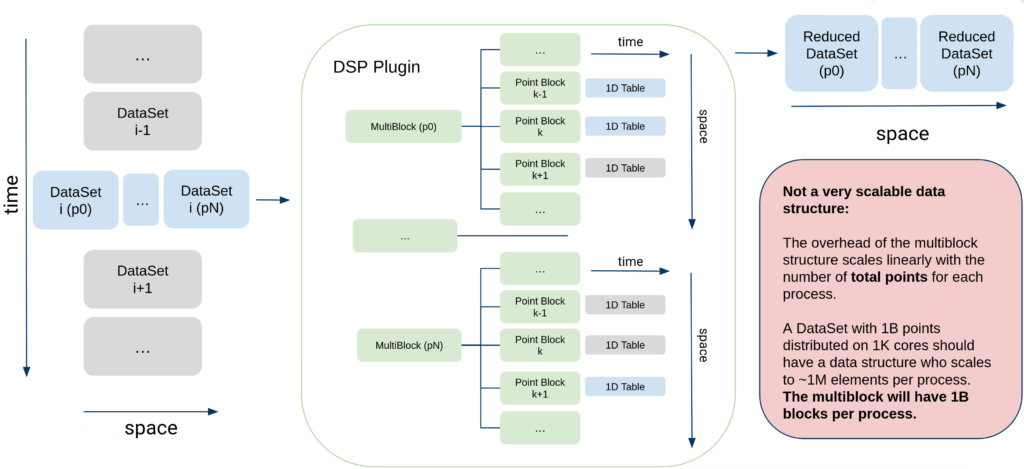
The usage of the multiblock data structure, while useful and easy to deploy at the time, is the cause of scalability issues and distributed computing issues.

Instead, the following “Multiplex” data structure was used:

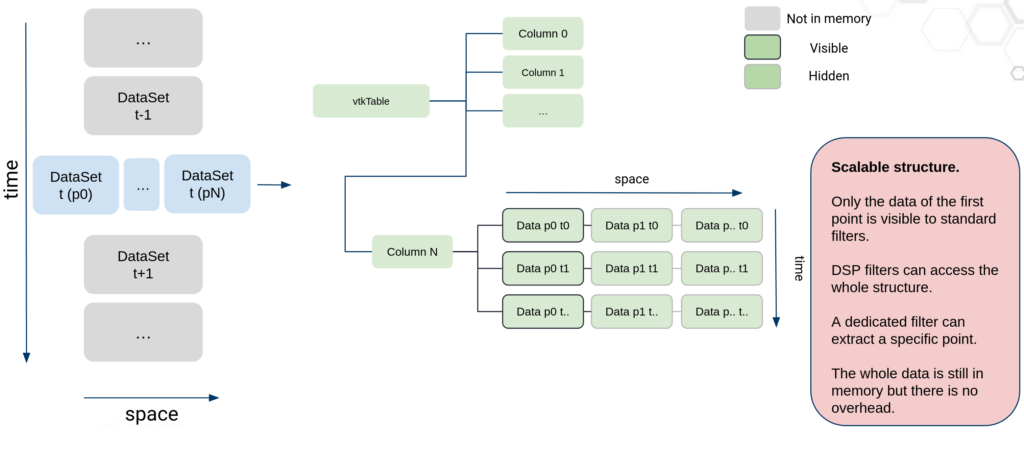
With this data model, we avoid all the overhead of using a composite data structure, increasing performance and making all the algorithms scalable and distributable. The classic VTK data model is able to handle millions of points in vtkPolyData and millions of rows in vtkTable, so this new model provides the same performance as long as the data can be stored in memory. This new model relies on multidimensional arrays to store both the temporal dimensions and spatial dimensions. The multidimensional arrays rely on the implicit arrays recently introduced in VTK. In short, these arrays are a very flexible framework to create new arrays from existing data while reusing memory.

A vtkTable contains multiple arrays, each of these arrays has a number of rows corresponding to the number of timesteps, we call it the temporal dimension, but it also has another dimension, corresponding to the number of points, we call it the spatial dimension.

To access the spatial dimension, one has to know that the array is multidimensional, if not, the array would appear as containing data for the first point only. To access and iterate through the hidden dimension, a specific accessor has been created and integrated into the different DSP filters.

Regarding data distribution, each processor will only operate on a subset of points – i.e a range over the spatial dimension
– avoiding any data supplication. If the original geometry was generated using ghost points, then each process still has access to ghost points as needed.

Some filters had to be specialized for this approach (especially DSP Table FFT) but a new generic approach has also been designed and integrated into VTK: the vtkForEach filter. This new “meta-filter” allows to iterate over a user defined sub-pipeline using different kinds of range (per block, per time step, …). You can find more information on how to use / extend vtkForEach in this discourse post.

Finally, keep in mind the Multiplex implementation of these filter are still compatible with the multiblock approach.

Benchmark of the Digital Signal Processing plugin

The objective of the benchmark was dual:

First, to compare the previous approach (using MultiBlocks through the Plot Data Over Time, i.e. PDOT) and the new approach (using multidimensional arrays through the Temporal Multiplexer, i.e. Multiplex).
Second, to evaluate the Multiplex solution speedup in the context of distributed computing.

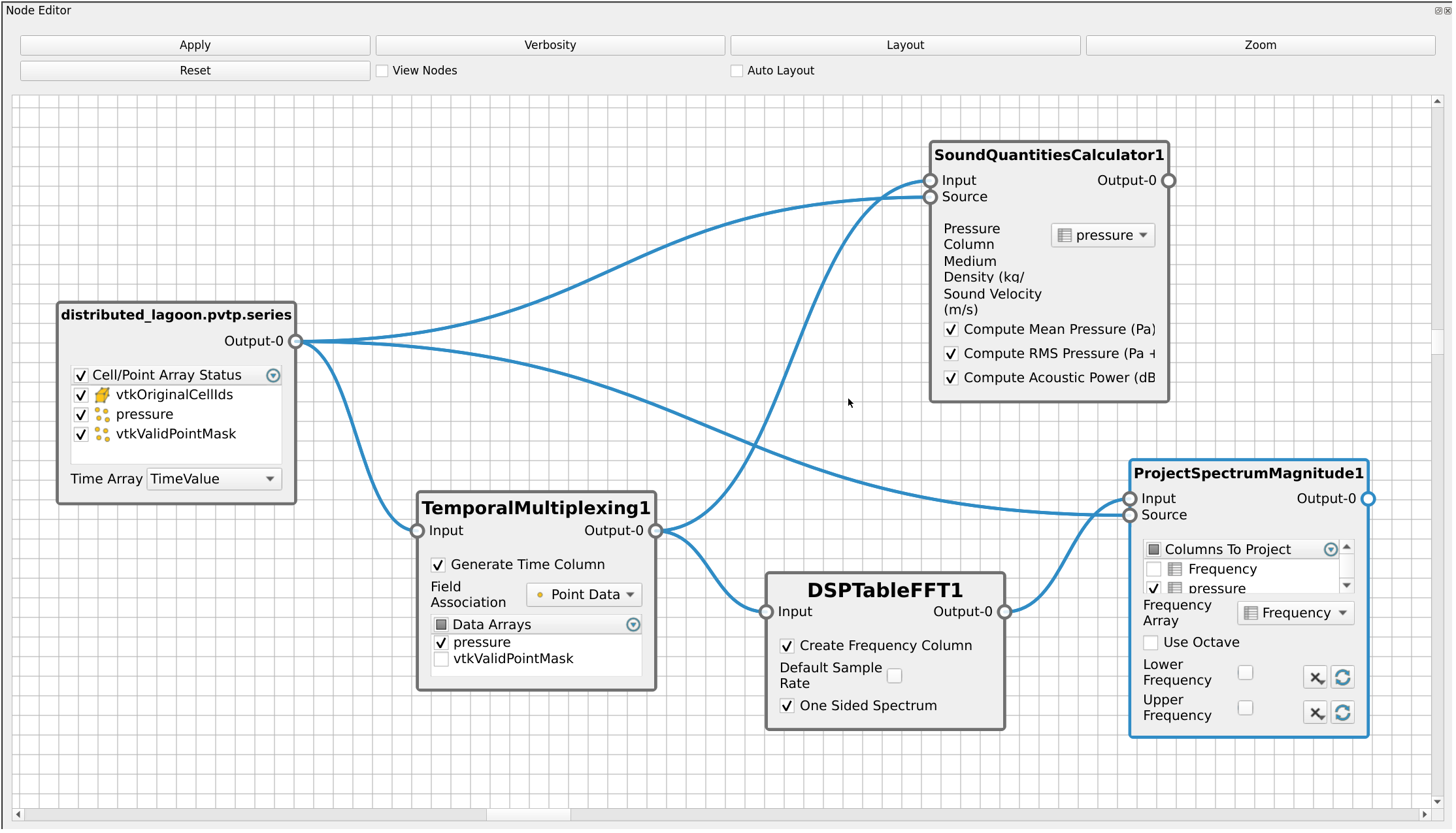
For our benchmark, we designed a classical acoustic pipeline with Sound Quantities Calculator, FFT and Project Spectrum Magnitude:

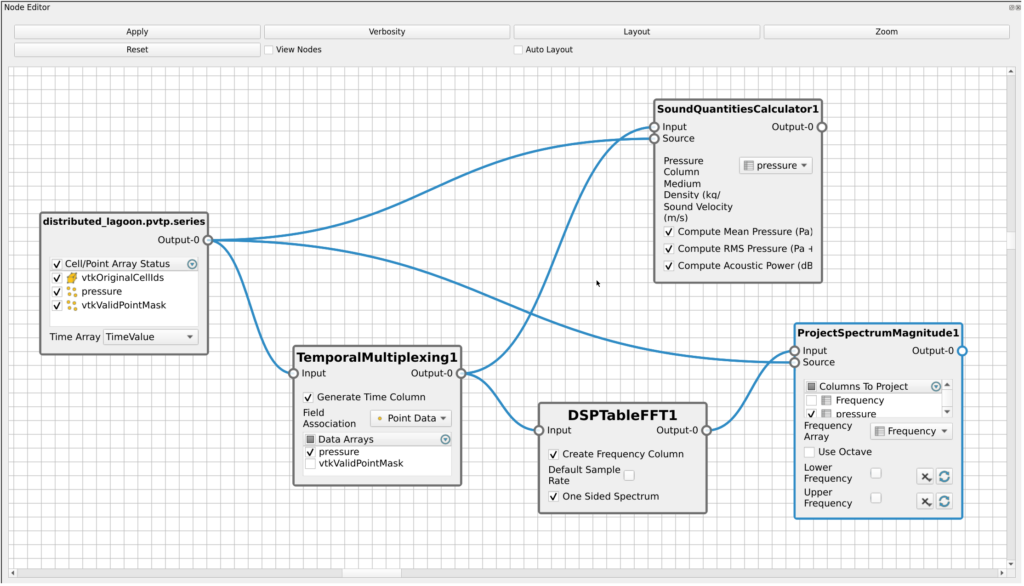
We decided to measure performance with an analytical procedural dataset with expected results where we could vary the number of points and number of timesteps easily and also avoid any I/O induced performance changes.

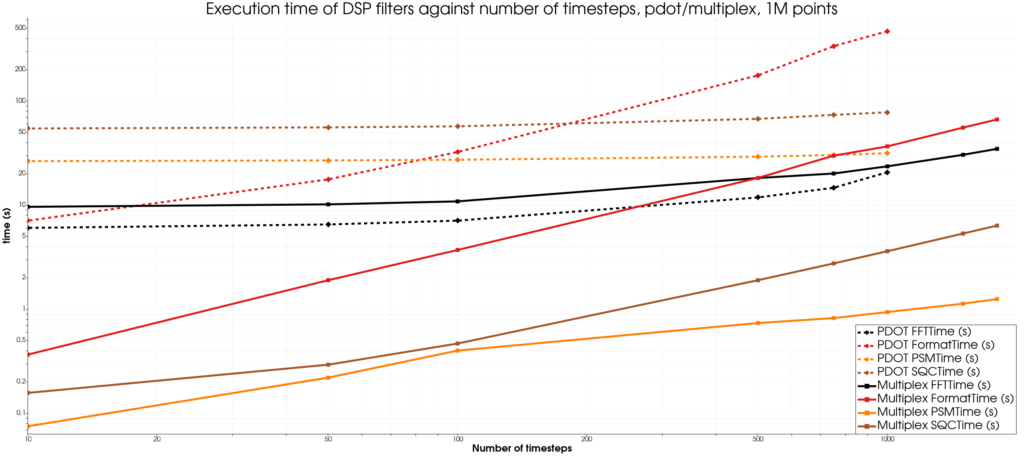
Of course, we also measured performances on small, medium and large industrial datasets which were kindly provided by our partners (see below). We varied the number of timesteps on the datasets but kept the geometry and number of points intact.

The benchmark scripts are open source and available in this repository. The industrial use case can be provided on demand if needed, and the analytical procedural case can be generated only using the scripts (see the README for more information).

The benchmark was run on dedicated powerful desktop computer without hyperthreading enabled or multithreading enabled on any of the computation.

CPU: 12th Gen Intel i9-12900K
16 cores : 8 P-core, 8 E-core
Max freq: 5.20 GHz

RAM: 128 Gib
4*32GiB DIMM DDR4

GPU: NVIDIA RTX A6000
48 GB GDDR6

Analytical results

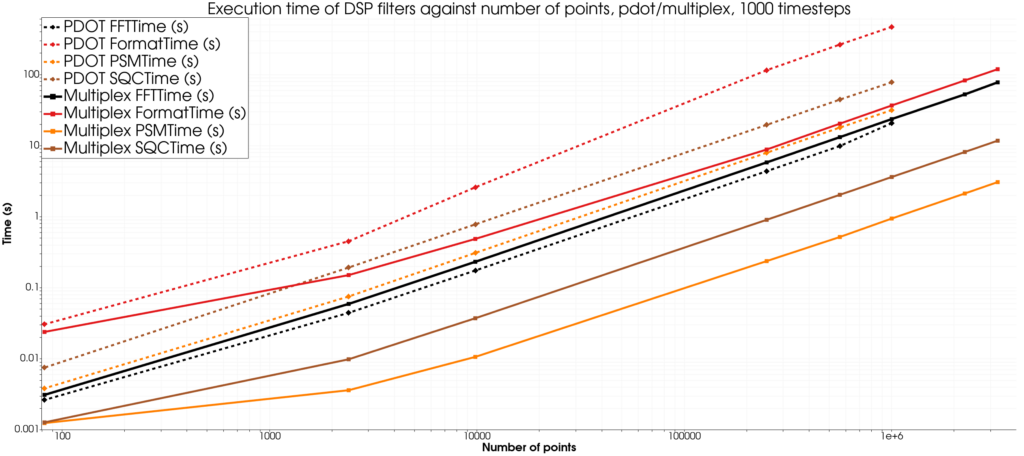
For the analytical dataset, we generate a sphere with harmonics varying over time. We make the number of points and the number of timesteps of the sphere change to generate each data point in the results.

As one can clearly see, the Multiplex approach outperforms the PDOT approach by one order of magnitude while showing linear growth when scaling the geometry and timesteps up, with the exception of the FFT filter.

Regarding memory usage, while we do not have precise measurement of the memory usage of each filter, the Multiplex approach used roughly half as much memory as the PDOT approach in the cases tested here, which is why the data is missing for the PDOT approach for the biggest case. This memory usage would theoretically scale worse and worse for the PDOT approach in a distributed context which would not be the case for the Multiplex approach.

More investigation should be conducted to understand why the FFT filter does not behave as well as other filters with the Multiplex approach, however, it looks like the Multiplex approach may win out on bigger datasets.

In short, this means that the Multiplex approach is perfectly usable in the context of large datasets, even without distributing the data.

But then, let’s test the Multiplex approach with distributed data.

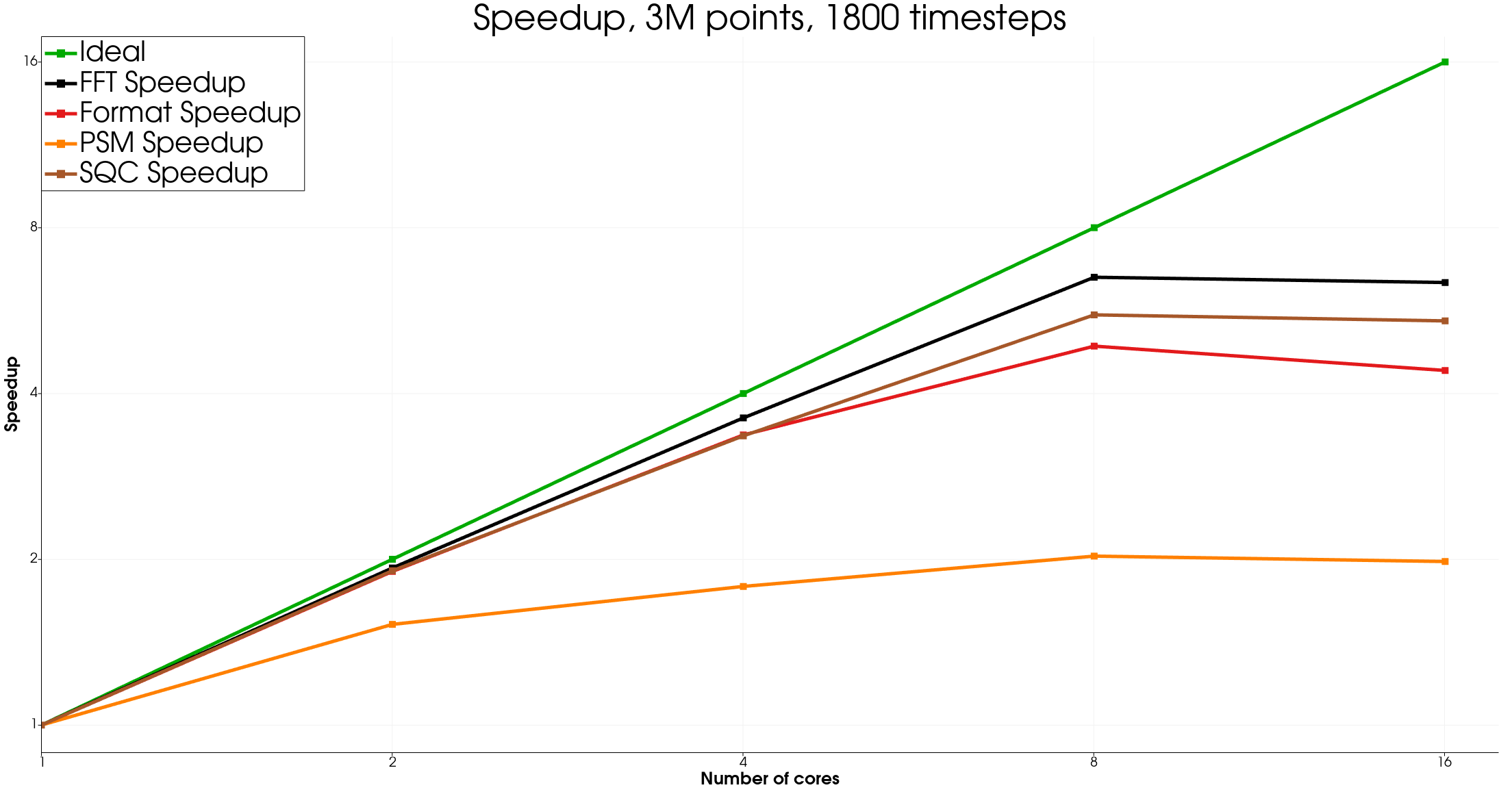
We can see good speedup for each of the evaluated algorithms, showing that our approach is perfectly adapted to distributed computing.

The 16 processes results are not great but can be explained by many reasons, the main one being the CPU in use (a consumer grade Intel processor containing both performance and efficient cores, not adapted to such a benchmark). More investigation would be required to understand this effect, by running this benchmark on a HPC environment.

Industrial datasets results

Let’s evaluate the performace of the Multiplex and PDOT approach with industrial, real, cases.

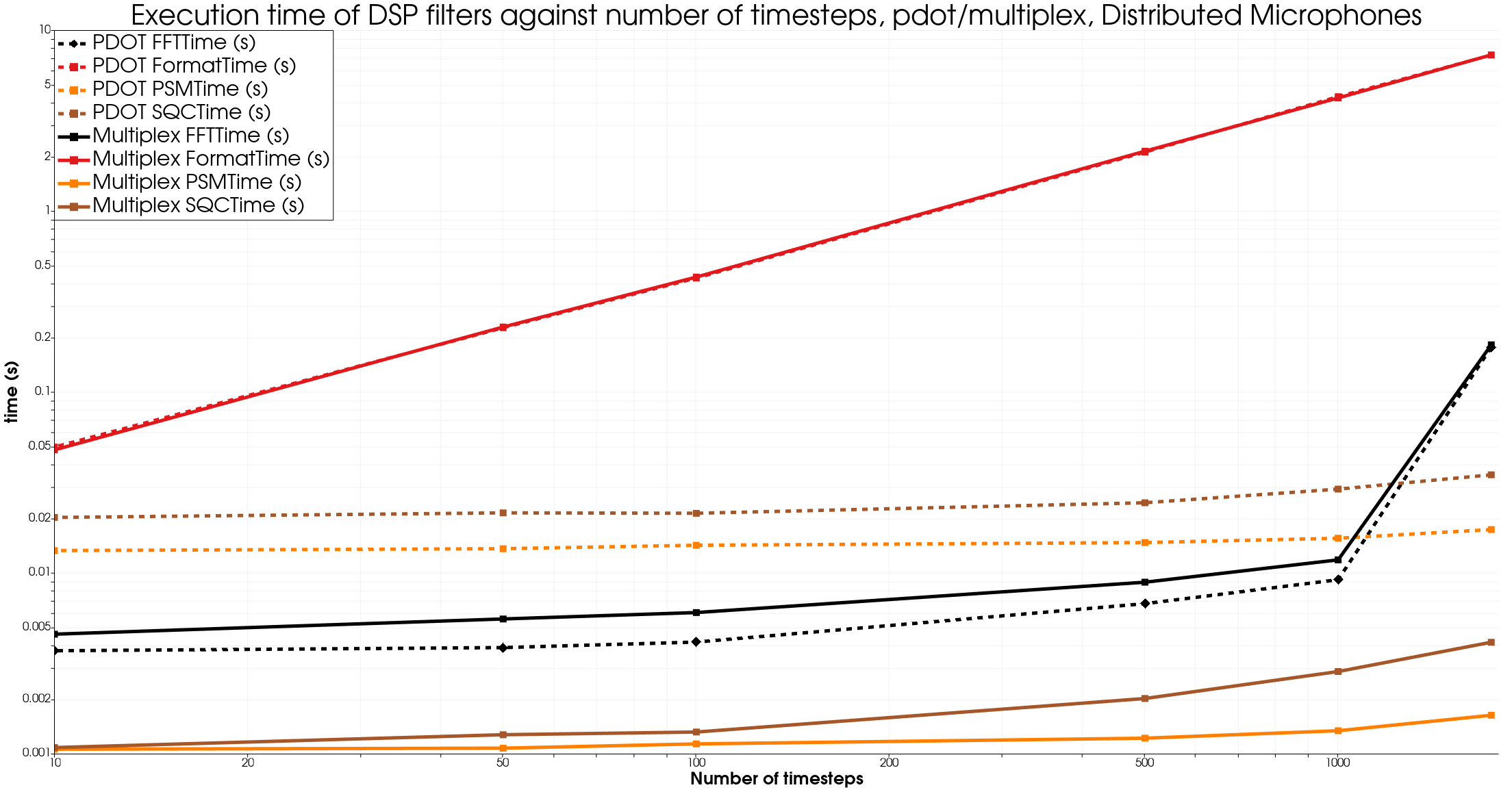
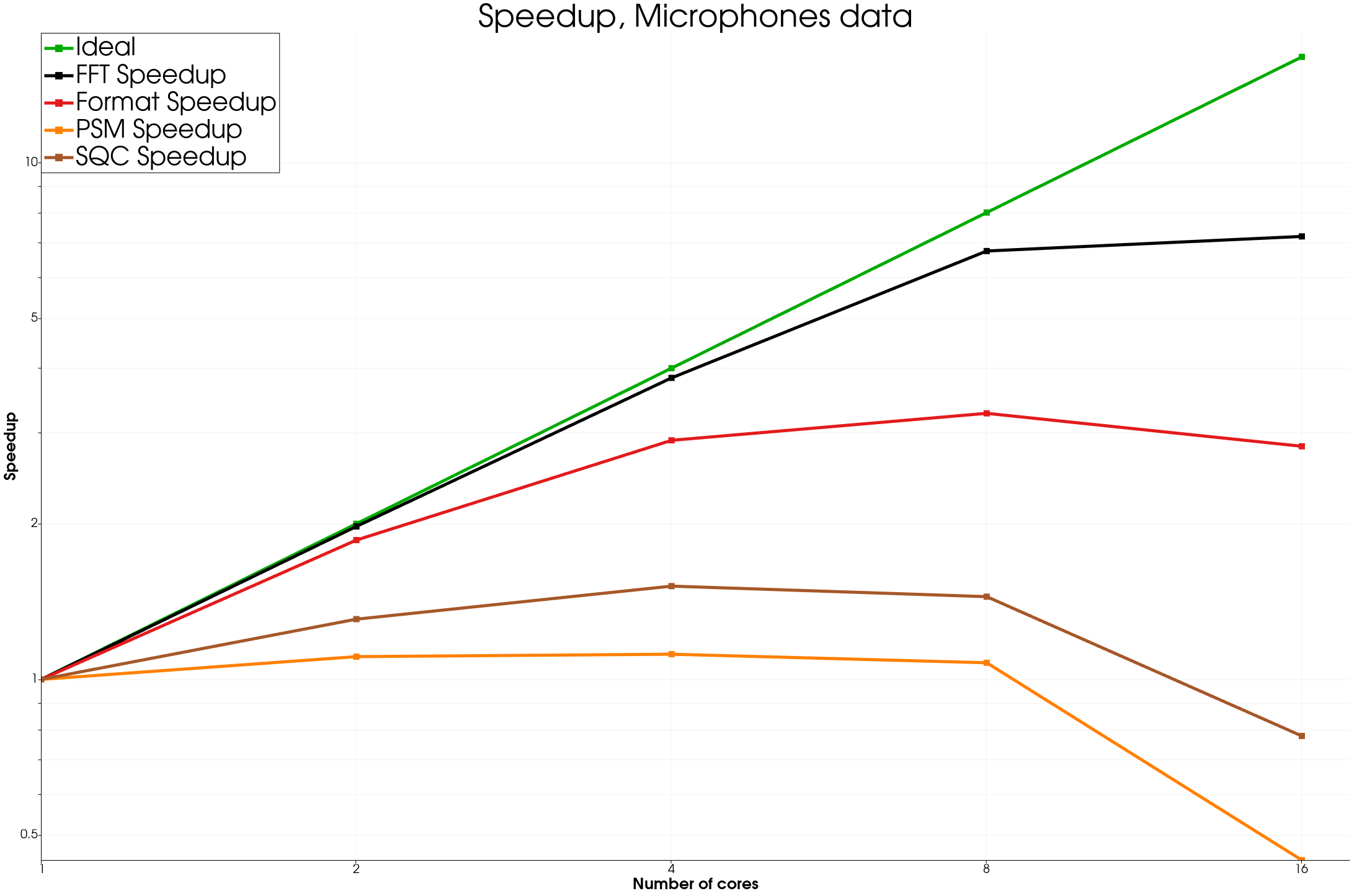
The small dataset, “Microphones” is a 500 microphone sphere with 1732 timesteps generated by microDB in the context of the CALM-AA project.
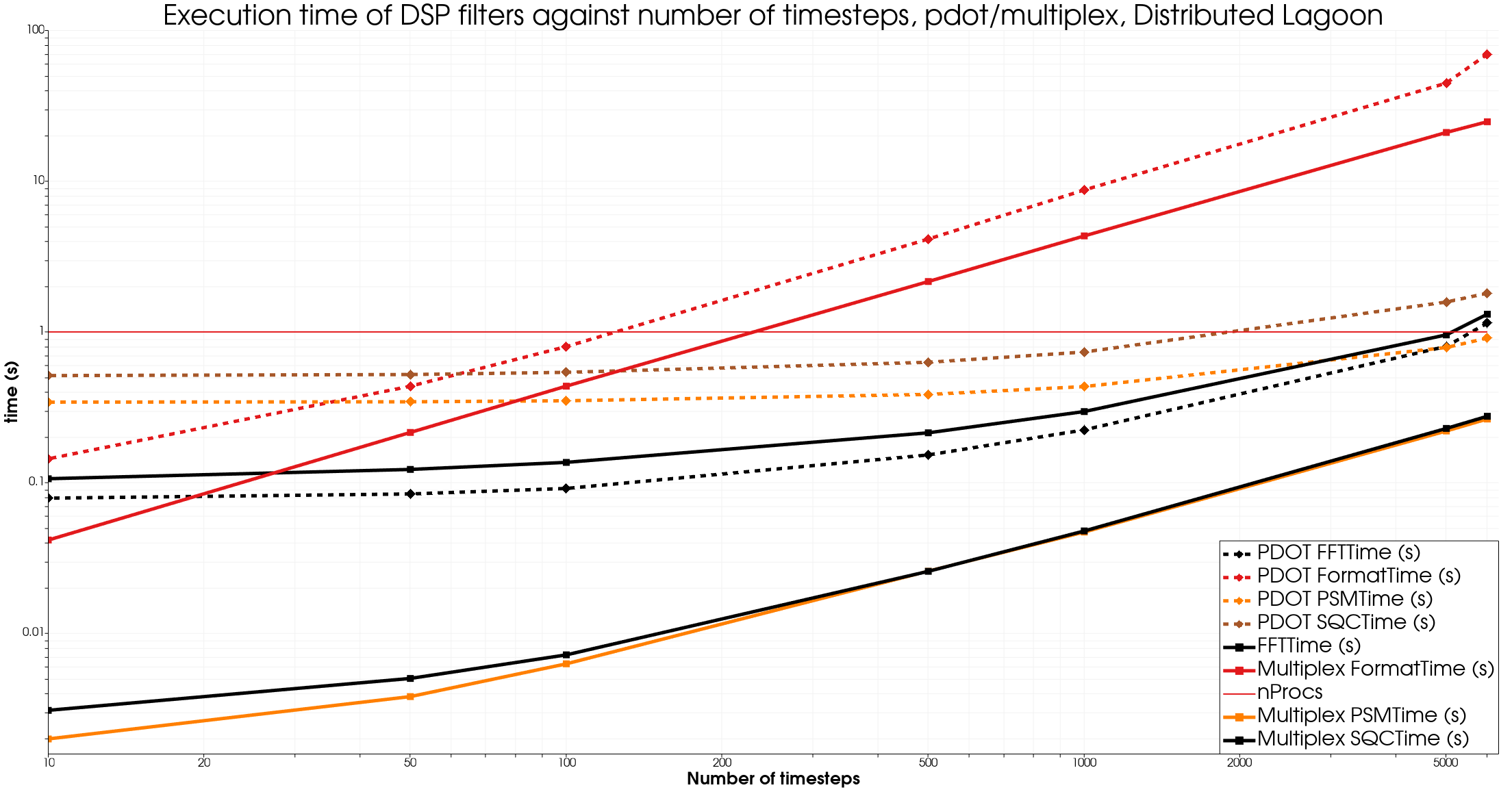
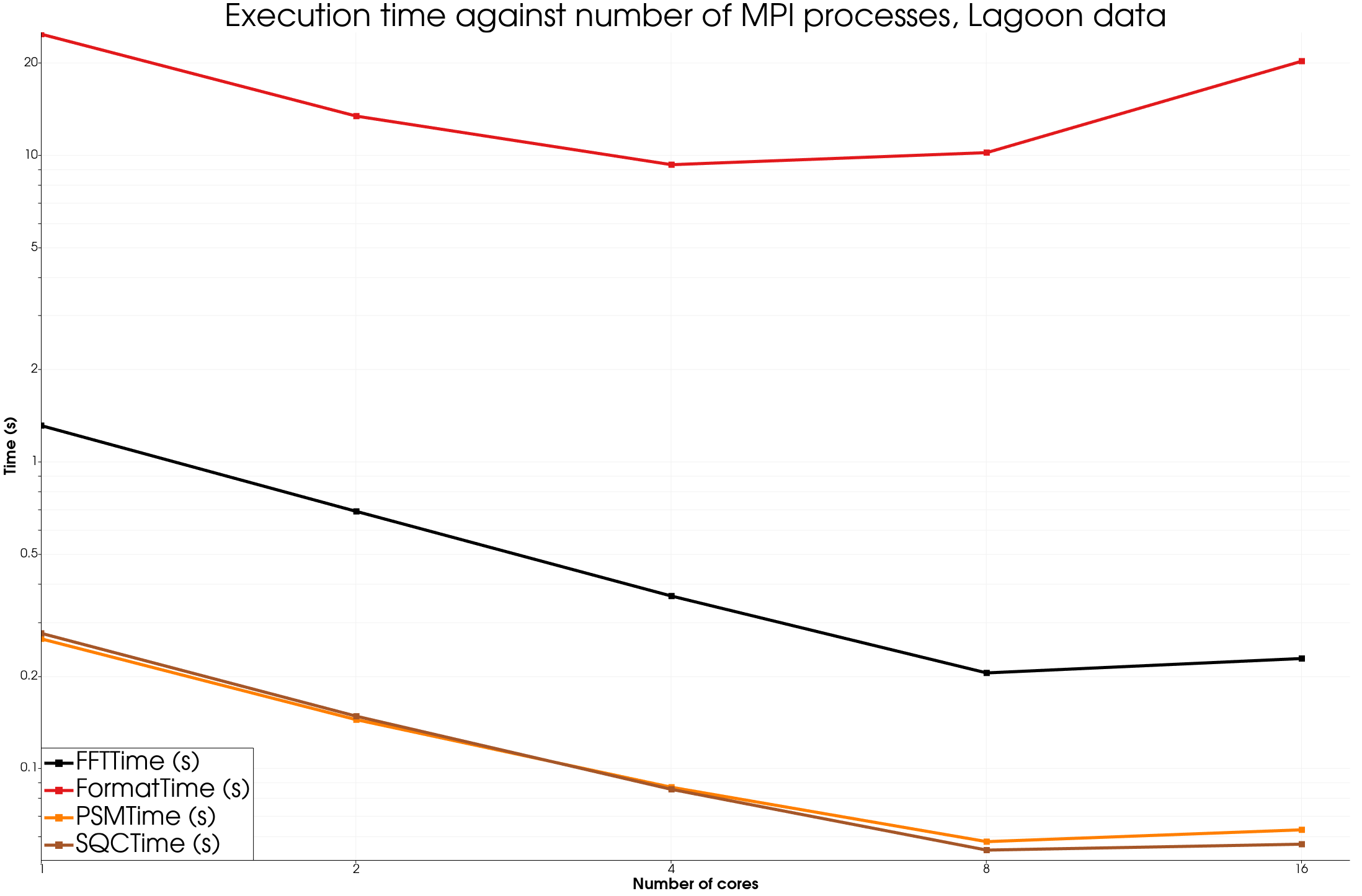
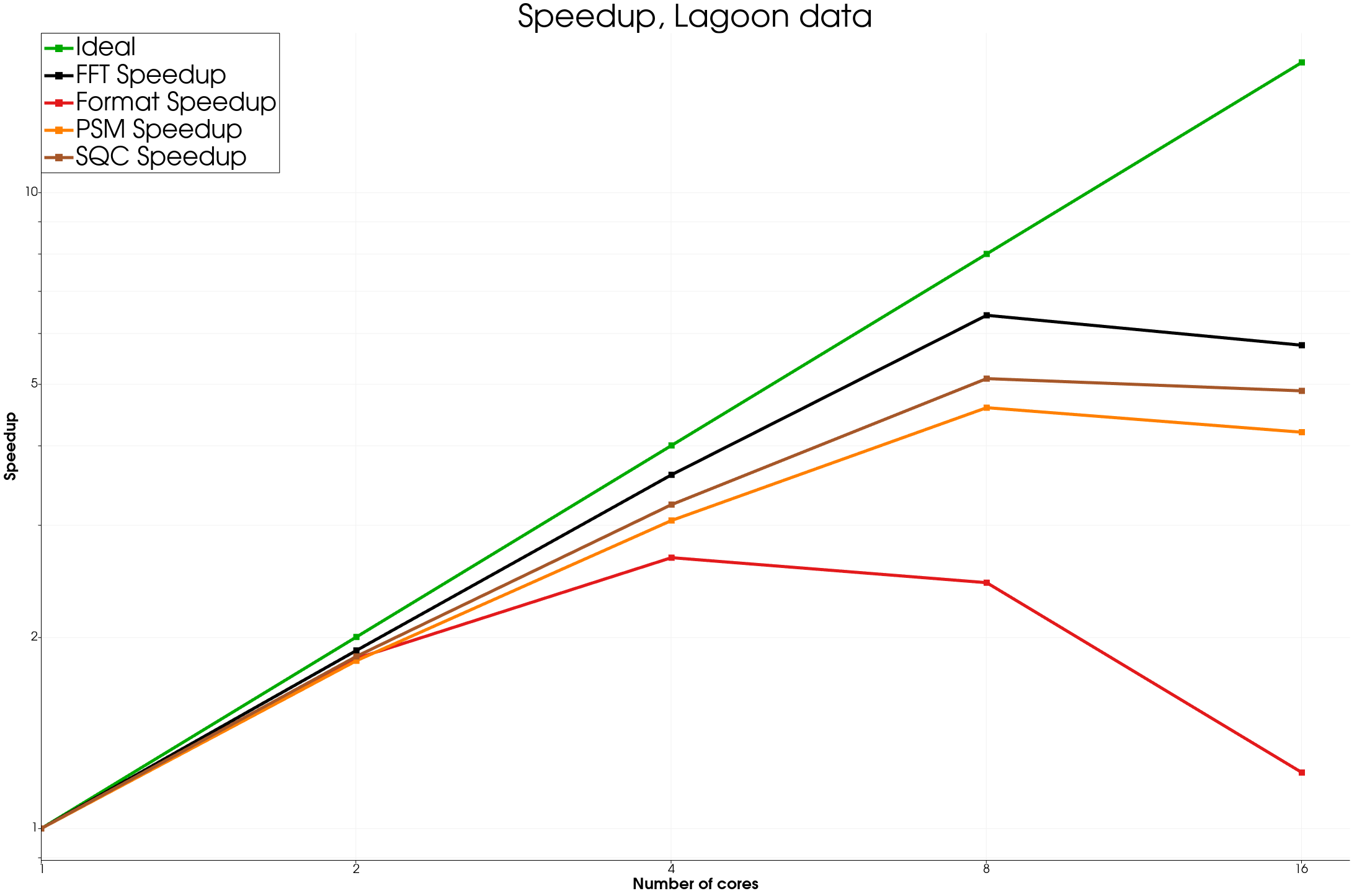
The medium dataset, “Lagoon” has 12778 points with 6000 timesteps and is a simulation of a plane landing gear generated by AIRBUS and shared by MicroDB in the context of the CALM-AA project.
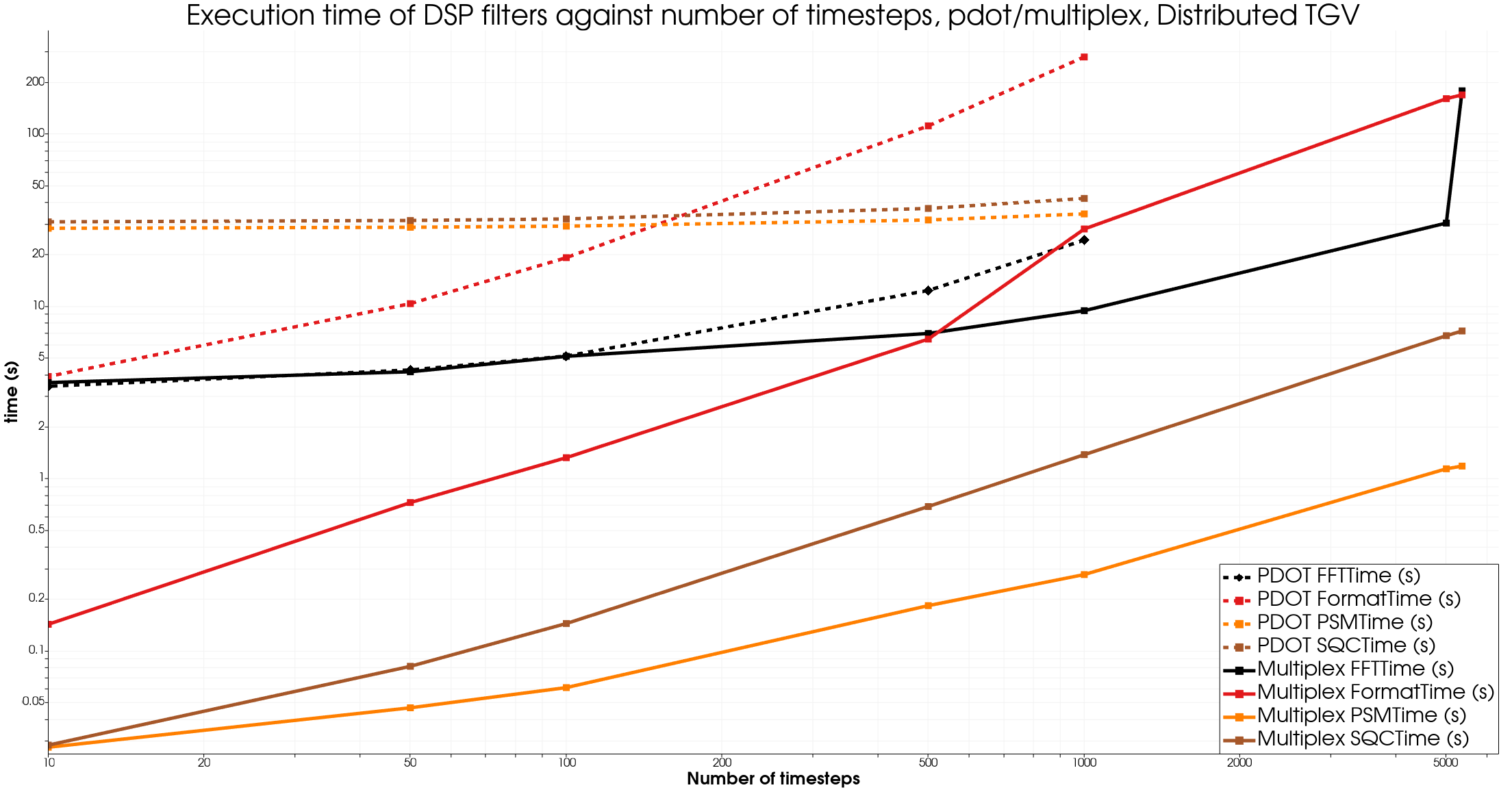
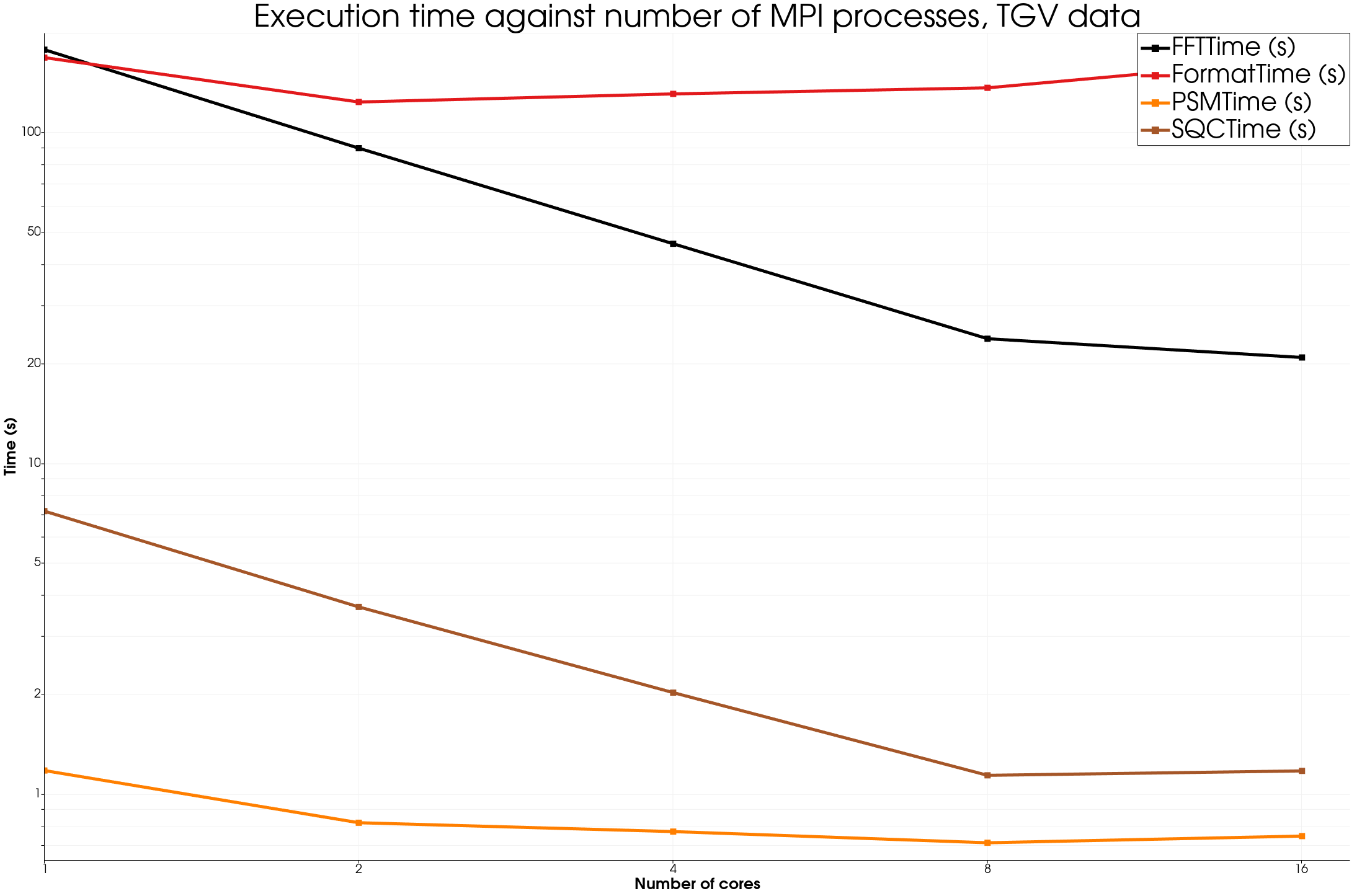
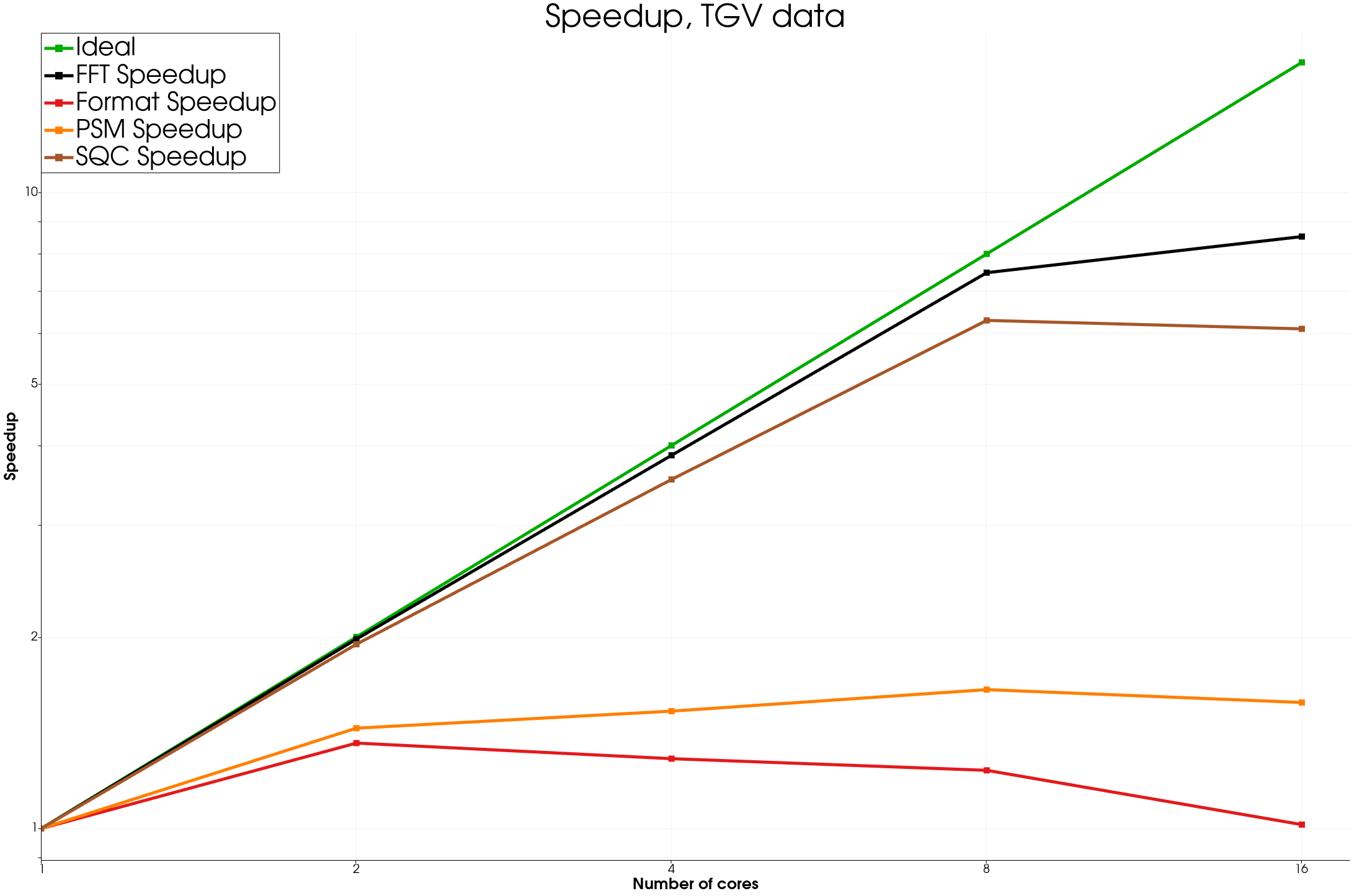
The big dataset, “TGV” is a 403804 point and 5364 timesteps simulation of a TGV simulated by KM Turbulenz.

The format time includes the I/O time.

On all datasets, once again we see strong improvements using the Multiplex approach, apart for the FFT filter for smaller datasets.

One interesting effect is that using the actual number of timesteps on the original dataset seems to trigger side effects in ParaView, probably caused by the VTK executive when iterating over all timesteps. More investigation would be needed to understand this effect fully.

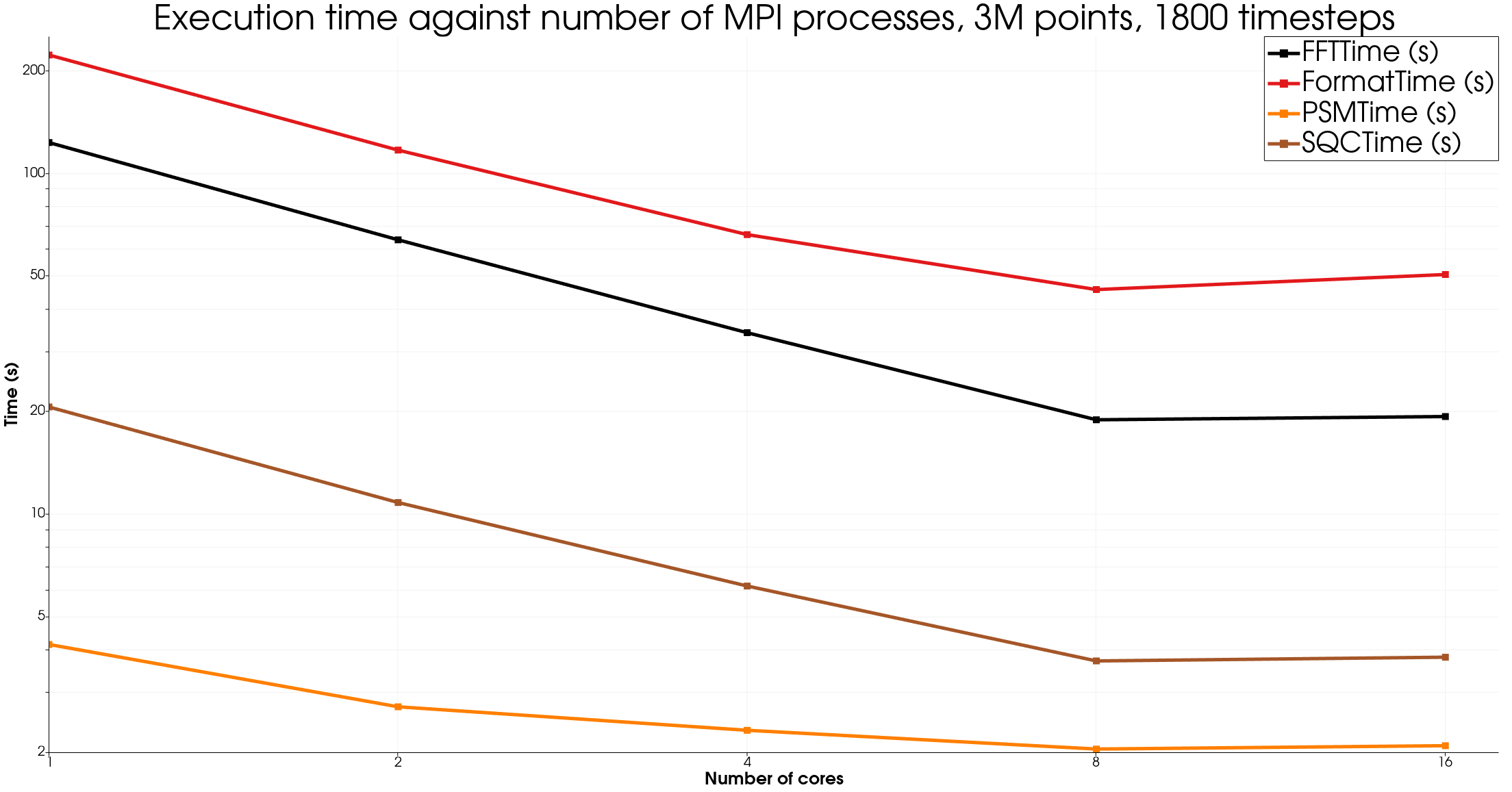
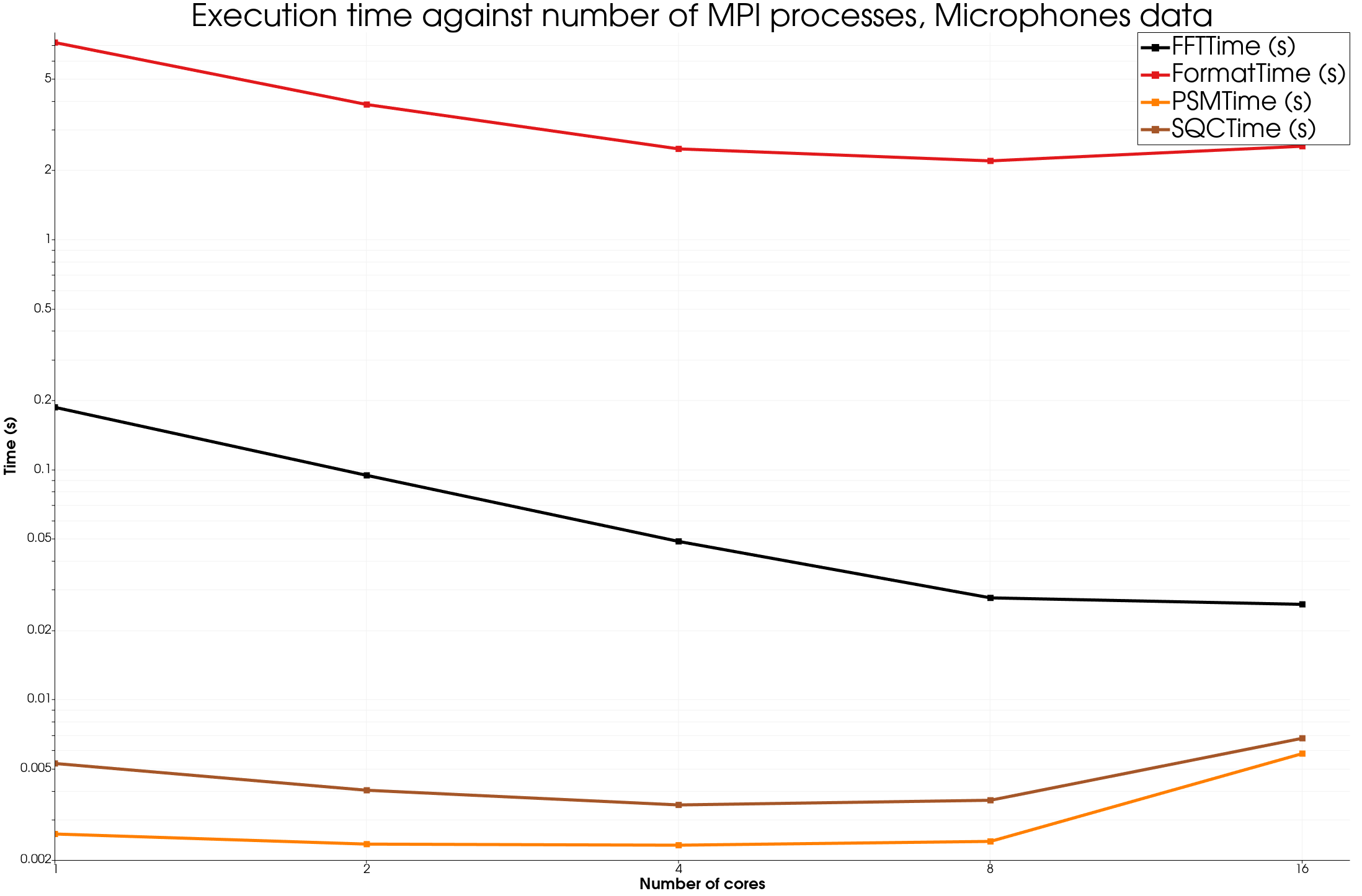
Now lets study how the different algorithm scales with more processors using the Multiplex approach

We see good speedup for most algorithms as long as the data is big enough. Of course, in the format time is included the time to read the data from disk, so there is not much speedup there, but using a distributed file system on a HPC system could be a way to improve such results.

We also remarked that in some cases the PSM time does not show a great speedup, more investigation would be needed, in any case, this algorithm is dominated by other algorithm in terms of computation time.

On the smallest dataset, Microphones, the speedup is not great but this is expected. On 16 processes, we see similar effects to the analytical results.

Once again, this proves that the Multiplex approach is perfectly compatible with ParaView’s distributed data approach.

Future improvements

This initial work on the DSP plugin has triggered a considerable amount of interest in the community and generated many avenues of prospective feature development and improvements. Some specific behaviors should be investigated and understood to see if further optimisations are possible, especially in regards to the FFT and PSM filter.

Many acoustic processing algorithms could be added in order to provide more tools for acoustic workflows.

The VTK_FOR_EACH prototype should be industrialized and integrated into the DSP plugin workflow, so that any filter processing on a single table could be used in the context of the Multiplex approach.

This work was funded by the CALM-AA European project (co-funded by the European fund for regional development).