Poisson Editing in ITK

Two very related problems in image processing are hole filling and compositing. This article explains an implementation of similar algorithms to solve both of these problems – poisson editing and poisson cloning; both algorithms were presented by Perez in “Poisson Image Editing”.

Poisson Editing/Hole Filling
First, we address the problem of image hole filling. The goal is to attempt to fill a missing region in an image so that the result looks plausible. The region can either actually be missing (in the case of a damaged photograph, or missing data in a digital file) or synthetically removed. In this example, our goal is to remove the jet from the following image, I:

To do this, we must manually specify the region to be removed with a hole mask, H:

In this implementation, non-zero pixels indicate the region to fill. As a sneak preview, the solution/resulting image is:

Theoretical Solution
It has been shown, using calculus of variations, that the best solution for the region inside the hole, H, is given by the solution to:

while ensuring H=I on the boundary of the hole. This setup is a Laplace equation with Dirichlet (also known as first order)
boundary conditions.

Discrete Solution
The continuous Laplace operator is given by:

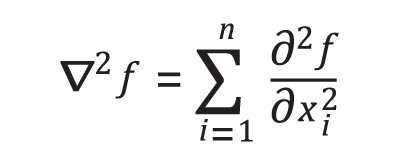
A common discrete approximation to this function at a pixel (x,y) is given by:

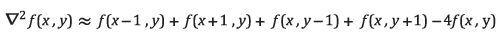
Another way to write this is by multiplying the pixel and its neighbors by a kernel K:

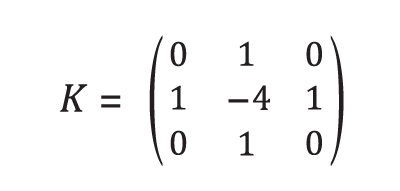
From there, for each unknown pixel u_i,j, the equation is:

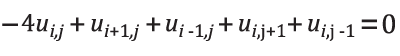
To solve the Laplace equation over the entire image, we can write a linear system of equations. Create a variable for every pixel to be filled; if the pixels are vector-valued (e.g. in an RGB image, the pixels are 3-vectors), N of these systems must be solved independently (where N is the dimensionality of the pixels) and stacked to produce the final result.

To solve the system of equations, a matrix U is constructed row-by-row, one row per variable. U is incredibly sparse, so a sparse solver should definitely be used. In each row, the value in the Laplacian kernel corresponding to the pixel’s location, relative to the current variable pixel, is placed in the column corresponding to the variable ID. When one of the pixels is on the border of the hole (and is therefore known), u(.,.) is replaced with p(.,.), the value of the pixel from the original image. In this case, rather than place the value of the Laplacian kernel in the U matrix, we instead multiply it by the image value and subtract the result from the corresponding entry of the b vector. That is, we move the known value to the right side of the equation.

A vector, H_v, the vectorized version of the solution to the set of hole pixels, is created as the unknown vector to be solved in a system of equations.

The linear system is then:

After solving for H_v, the resulting H_v is then remapped back to the pixels corresponding to each variable ID to construct H.
In this implementation, the UMFPACK interface provided by Eigen3 is used to perform the computations. On a single channel image, approximately 500×500 in size, the hole filling procedure takes only a few seconds.

Code Snippet
We have packaged this implementation in a class called PoissonEditing. Using this class is very straightforward. The image and mask variables must be set and the FillMaskedRegion() function does the work. If the image consists of vector-valued pixels, it is internally decomposed, filled, recombined, and returned by the GetOutput() function.

PoissonEditing<ImageType> editing;
editing.SetImage(image);
editing.SetMask(mask);
editing.SetGuidanceFieldToZero();
editing.FillMaskedRegion();

ImageType* outputImage = editing.GetOutput();

GUI
A Qt GUI is provided to allow users to easily load an image/mask pair, fill the hole, and inspect the results.

Region Copying
In the problem of region copying (a.k.a. seamless cloning or compositing), we are interested in copying a region from one image into another image in a visually pleasing way. Again, this is best motivated with an example. In our example, the goal is to copy the jet from the Poisson Editing example into the image of the canyon shown below:

The final result in shown below:

Concept
In Perez’s original paper, it was argued that a good way of copying a region from one image into another image is to do something very similar to hole filling, but with the additional introduction of a “guidance field,” G. That is, the way to copy a region from one image into another is by solving the equation:

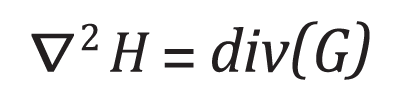
The boundary condition is again first order and specifies that the resulting H be equal to the target image, T, at the hole boundary.

The suggested guidance field G is the gradient of the source image. That is:

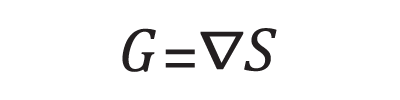
In this case, the right-hand-side of the equation has become exactly the Laplacian of S.

Discrete Solution
Just as before, the discrete Laplacian equation is written for each pixel, but this time the right-hand-side is set to the Laplacian of S at (i,j), rather than 0. When the right side of this equation is non-zero, it is referred to as a Poisson equation rather than a Laplace equation. The equation for each pixel is now:

The linear system:

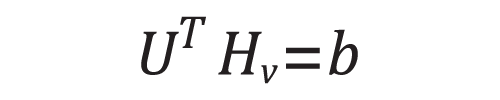
is created and solved identically as before.

Code Snippet
We have implemented this functionality in a class called PoissonCloning. Using this class is very straightforward. In fact, PoissonCloning derives from PoissonEditing and the only addition is that PoissonCloning provides a SetTargetImage function. The rest of the functionality is identical.

PoissonCloning<ImageType> cloning;
cloning.SetImage(sourceImage);
cloning.SetTargetImage(targetImage);
cloning.SetMask(mask);
cloning.PasteMaskedRegionIntoTargetImage();

ImageType::Pointer outputImage =
  cloning.GetOutput();

GUI
A Qt GUI is in the works to allow users to easily load an image/mask pair, fill the hole, and inspect the results.

Image Manipulation in Gradient Domain
There are many image processing techniques that involve manipulating the gradient or Laplacian of an image. After these manipulations, it is usually necessary to return the result to the original image domain. While these operations are not necessarily related to image hole filling or cloning, we have already presented the framework needed to solve this problem, so we will explain how to use it.

To return to the image domain from the gradient domain, one must find the least squares solution to a system of equations involving the derivatives of the image; however, this technique is not often used. More commonly, the derivatives are first combined into the Laplacian. We will describe the procedure for both methods below.

Reconstructing Images from Derivatives
For the task of reconstructing an image directly from its derivatives, we can use a method that is very similar to solving the Laplace equation. This time, however, there are two equations to be solved simultaneously:

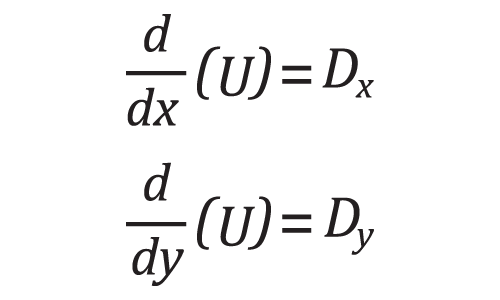
where D_x and D_y are the known derivative images. Of course, the first order boundary conditions must be known. This time the boundary is the actual border of the image. To relate this back to the Poisson concepts, what we are doing is using the entire inside of the image as the “hole,” the image gradients as the guidance field, and the image boundary as the hole boundary.

We can construct the same type of linear system to solve for the components of U that best satisfy both equations. Any discrete derivative operator can be used. We have chosen to use the Sobel operators:

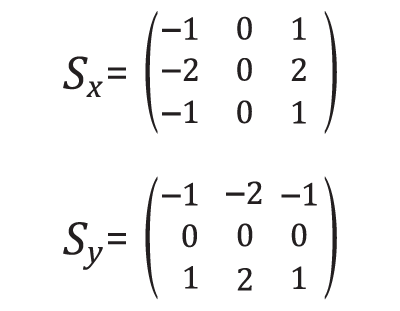
By applying these operators to every pixel in the unknown image U, we can write a system of equations, two
for each pixel:

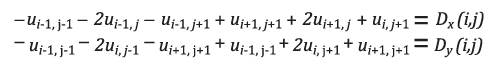
Again, we simply place the coefficient of each term in the column of the matrix that corresponds to the variable ID of the pixel. As usual, we move the term to the right side of the equation (to contribute to the b vector) if the pixel is known. Below we show an image, its derivatives, and the image reconstructed using only the border of the image in and the derivatives.

We have provided this implementation in a file called DerivativesToImage.cxx.

Reconstructing Images from Laplacians
The technique for reconstructing an image from its Laplacian is even more similar to Poisson Cloning than the reconstruction from derivatives. We specify the Laplacian in the non-boundary region as the guidance field. We’ve provided this implementation in a file called LaplacianToImage.cxx.

Conclusion
We have presented the concept of Poisson image editing as well as described an implementation using ITK and Eigen3. The intention is to serve as a reference implementation, as well as a springboard for future research in these areas.

David Doria is a Ph.D. student in Electrical Engineering at RPI. He received his B.S. in EE in 2007 and his MS in EE in 2008, both from RPI. David is currently working on hole filling in LiDAR data. He is passionate about reducing the barrier of entry into image and 3D data processing. Visit http://daviddoria.com  to find out more or email him at daviddoria@gmail.com.