Python Module to Create Weighted Functional Box Plots

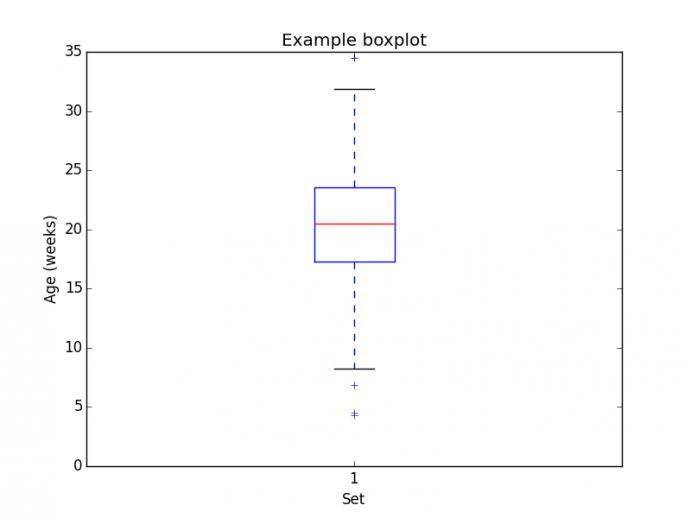
With simple zero-dimensional data, basic statistics of a population can be displayed with a boxplot. A boxplot shows the median, interquartile range, and outliers in a population described using single scalar values. For example, you can plot the distribution of ages for a random sampling of 40 individuals. The boxplot shown below enables you to identify the median age, the interquartile range, and individuals who are outliers. The boxplot is an effective way to represent statistics about a population via the actual measurements from individuals within that population.

For our work on the project "Predictive Modeling for Treatment of Upper Airway Obstruction in Young Children" with collaborators at UNC, we are working with one-dimensional curves that represent airway cross-sectional area as a function of depth in the airway. A challenge with this data is to compute and display statistics over the population of curves. One might consider creating a point-wise average curve to represent a typical airway, but this might smooth out the data and produce a representation that is not reflective of any one individual. The same is true if we estimate airway typicality with a point-wise median/interquartile range calculation along all the curves.

An alternative solution uses individual curves from the population to represent the population median and interquartile range. This method relies on the calculation of a quantity for each curve called the "band depth". The band depth is essentially a measure of how often one curve is bounded above and below by other curves in a set. The curve with the highest band depth is considered the "most typical" and is equivalent to the median. The interquartile range for the functional boxplot is the region bounded by the top half of the curves, ranked by band depth.

This project has led to the development of the weighted functional boxplot [1]. A weighted functional boxplot assigns a weight to each curve in the population based on some attribute associated with the curve, e.g., age in months. This weight is used when determining band depth. The advantage of the weighted functional boxplot is that it can be used to adapt the statistics to a smaller segment of the total population. For the cross-sectional area curves, this can be used to visualize the airway statistics of 30-month-old children by putting a large weight on the curves from individuals who are close to 30 months old and smaller weights on curves from individuals much younger or older than 30 months.. In the weighted functional boxplot, the interquartile range is determined by the curves with the highest band depth that make up 50% of the population weight. Note that this is not necessarily half of the curves.

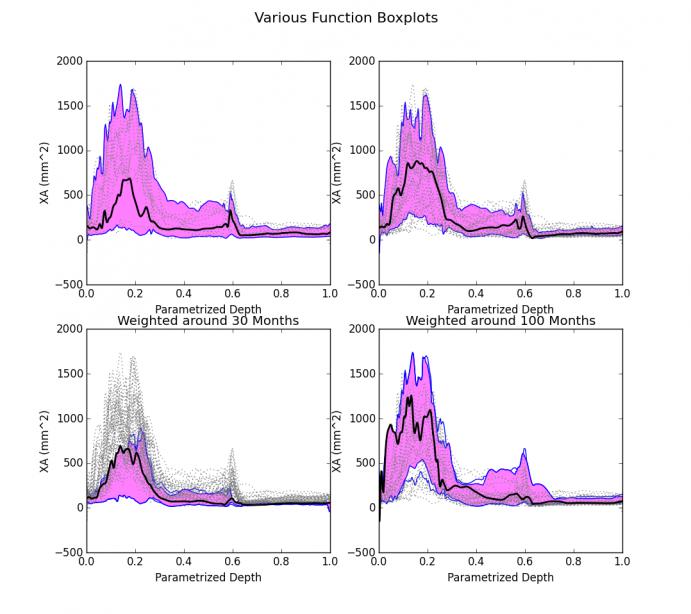
Though there was an existing module to generate unweighted functional boxplots, it was not possible to apply weights or use different methods to calculate band depth. We have developed a python module called AtlasBuilder that can do both of these things. Below you can see a set of functional boxplots produced from identical data using different generation algorithms.

The top row represents the results from two separate algorithms to calculate band depth with no weighting. The bottom row shows the plots for the population of 30-month-olds and 100-month-olds respectively. Note the overall increase in cross-sectional area for the 100-month plot. The black curves are the medians of each plot. The dotted lines are outliers. The magenta region is the area bounded by the curves that represent the interquartile range. The blue lines are not actually curves from the population but are the point-wise upper and lower bounds generated from the curves that envelope the magenta region. In the weighted functional boxplots there are two blue lines visible outside of the interquartile region. These lines indicate the region bounded by the curves with 99.7% of the population weight. 

The data that went into these graphs was generated from the cross-sectional area of the airways from control subjects derived from CT scans. The curves are registered using several anatomical landmarks so that each anatomical landmark is at the same parametric depth along the curve for each individual in the population.

The project described was supported by Grant Number R01HL105241 from the National Heart, Lung, And Blood Institute.  The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Heart, Lung, And Blood Institute or the National Institutes of Health.

References

[1] Hong Y, Davis B, Marron JS, Kwitt R, Singh N, Kimbell JS, Pitkin E, Superfine R, Davis SD, Zdanski CJ, Niethammer M, Statistical Atlas Construction via Weighted Functional Boxplots, Medical Image Analysis. 2014 May;18(4):684-98.