Really Fast Isocontouring

Introduction

For the last several years, the VTK community has been working hard to improve system performance. These changes impact not only VTK, but the hundreds of applications and frameworks that depend on VTK such as ParaView, 3D Slicer, and trame. In this post we’d like to focus on one of the most important classes of algorithms: volumetric isocontouring.

Marching Cubes (MC) popularized the importance of volumetric isocontouring when the paper was published in 1987. Originally designed to visualize isosurfaces from MRI and CT scans, the simplicity and elegance of the algorithm produced a reference article that is reputedly the most highly cited paper in the visualization literature. The algorithm has since been redeployed to address other important application areas such as climate studies, simulation, geometric modeling, anatomy, and even geological exploration. In VTK, the class vtkMarchingCubes was one of the first algorithms implemented in the system, and is continued to be used to this day.

Marching Cubes, despite its widespread impact, suffers from several performance-related limitations. Written as a sequential algorithm, it does not scale well due to inherent bottlenecks and data access inefficiencies, which hampers its use in parallel applications. This is particularly noticeable as volumes grow in size — nowadays in some cases such as connectomics, huge volumes on the order of 20,000³ [BossDB] are created. The algorithm also focuses on just one type of data, that is the algorithm is designed to isocontour continuous scalar fields such as CT Hounsfield units, temperature, density, or distance fields. This leaves out an entire type of important data typically referred to as segmentation, label, or annotation maps which are discrete scalar fields in which each voxel is labeled according to membership in some set. For example, a label map may identify which voxels lie in different parts of the brain.

While Marching Cubes has been modified to address discrete scalar fields (see vtkDiscreteMarchingCubes), not only does it retain the performance limitations of the base algorithm, it produces results that are problematic. Notably, while the output data shares points across object boundaries, triangles are duplicated on region boundaries. These limitations are particularly aggravating as data size continues to grow, medical simulation is increasingly important, and with the emergence of widespread AI-based, automated segmentation systems such as TotalSegmentator discrete isocontouring is an increasingly important application.

With these considerations in mind, there has been a growing need to create faster algorithms which leverage parallel computing technologies and provide solutions for both continuous and discrete isocontouring applications.

vtkFlyingEdges3D and vtkSurfaceNets3D

To address these and other MC limitations, the VTK community has developed two notable parallel algorithms: Flying Edges (FE) and the recently contributed Parallel SurfaceNets algorithm (PSN) (implemented as VTK classes vtkFlyingEdges3D and vtkSurfaceNets3D). (Note that the original, sequential Surface Nets algorithm was created by Sarah Frisken.) These are performant, threaded algorithms addressing the two major classes of volumetric isocontouring: continuous scalar fields (vtkFlyingEdges3D), and discrete scalar fields (vtkSurfaceNets3D). Both of these algorithms are now available in VTK’s master branch, and use vtkSMPTools with which to implement these shared memory, threaded algorithms. Depending on the particulars of a computing system (OS/compiler, memory, bus, number of threads, vtkSMPTools backend), performance studies indicate that the algorithms are one to two orders of magnitude faster than the basic marching cubes algorithm. (As far as we know, these are some of the fastest, if not the fastest, non-preprocessed isocontouring algorithms available.)

Why so much faster? While we’d love to nerd out here and go into excruciating detail (the source code is of course available in VTK), we’ll try and narrow it down to a few key points.

• Marching Cubes (MC) processes volumetric data by accessing voxel cells (the so-called cubes in MC). Since a voxel cell is formed by combining eight voxel values at the vertex corners, the result is that each voxel value may be accessed up to eight times, and each voxel cell edge may be processed (i.e., edges intersected) up to four times, for interior voxels during algorithm execution.
• VTK’s Flying Edges and Surface Nets (SN) algorithms process volume edges. This means that threaded, independent processing of data along each edge can occur, so that in most cases, voxel values are accessed only one time, and edge intersections are performed only once.
• Point merging is eliminated. In many MC implementations, duplicate points are eliminated by using some form of hashing (geometric or topological). This results in a bottleneck that is detrimental to high-performance, parallel algorithms. Both Flying Edges and Surface Nets eliminate this bottleneck by using a clever edge-based iterator to generate output points and triangle cells.
• Marching Cubes requires adaptive, incremental memory allocation. Since it is generally not possible to predict the size of the output during MC execution (since the output size is a function of the data and isovalue), as the algorithm executes it incrementally generates and inserts points and triangles, requiring adaptive memory allocation. Repeated memory allocation is typically quite slow.
• Flying Edges and Surface Nets are multi-pass algorithms. Many non-trivial parallel algorithms are designed around multiple data passes. There are several advantages to this approach: simplicity, often cache-coherence improvements, and one time memory allocation. In FE and SN, initial passes are made which prepare and gather information about the output. This enables the algorithms to precisely allocate memory only once, and use multiple threads to simultaneously produce output.

While extremely fast, like many threaded, shared memory algorithms, both FE and SN suffer parallel efficiency declines as the number of threads increase (which is mostly due to saturation of the memory bus, cache locality issues, and/or thread overhead). While this behavior is a function of the computing platform, on our test systems these effects typically show up as the number of threads approaches 20-40 CPU threads. (Note: Robert Maynard has implemented FE in vtk-m [https://www.osti.gov/servlets/purl/1408391] which of course has very different performance characteristics.)

Some Examples

Here are some examples of both Flying Edges and SurfaceNets in action. As mentioned previously, performance improvements are typically one to two orders of magnitude greater than MC-based algorithms, depending on the number of threads used, and the particulars of the computing platform. Note that even when running in sequential mode (i.e., one processor), both VTK’s Flying Edges and SurfaceNets algorithm are significantly faster than Marching Cubes. (For performance details, see the references listed previously.)

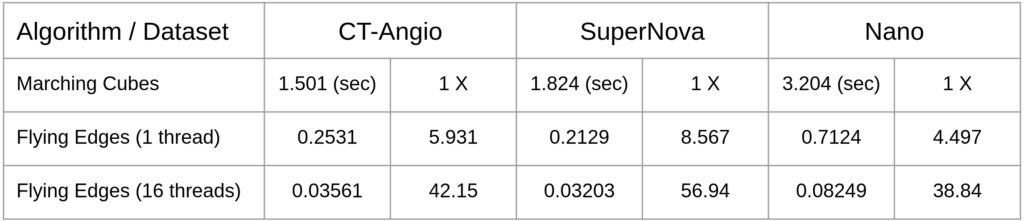
Flying Edges. Three datasets are shown in the figure below. The first (CT-Angio) is an anonymized CT angiography scan at resolution of 512² × 321, with 16-bit (continuous) scalar values and isovalue q=100. The next test dataset (SuperNova) is simulation data 432³ with a 32-bit float scalar type. The isovalue was set to q = 0.07. And finally, the (Nano) is a scanning transmission electron microscopy dataset of dimensions (471 × 957 × 1057) with q = 1800 and 16-bit unsigned scalars.

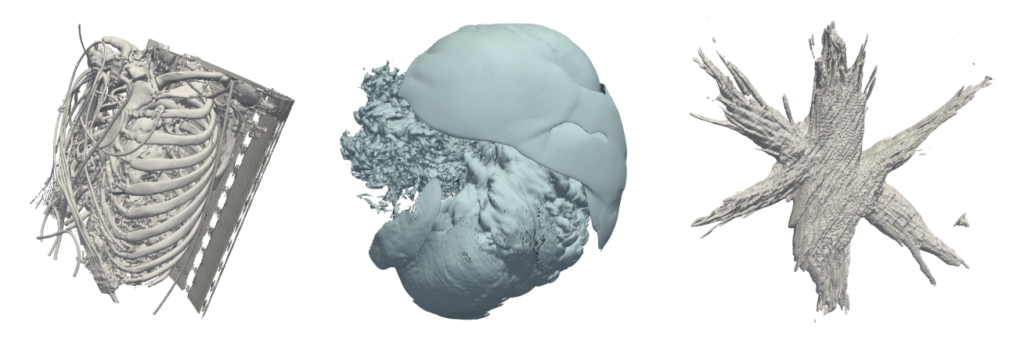
Execution time and speed up factors for these three datasets are tabulated below with the maximum number of threads set to 16. Note that Flying Edges is much faster than Marching Cubes even when run sequentially (with one thread).

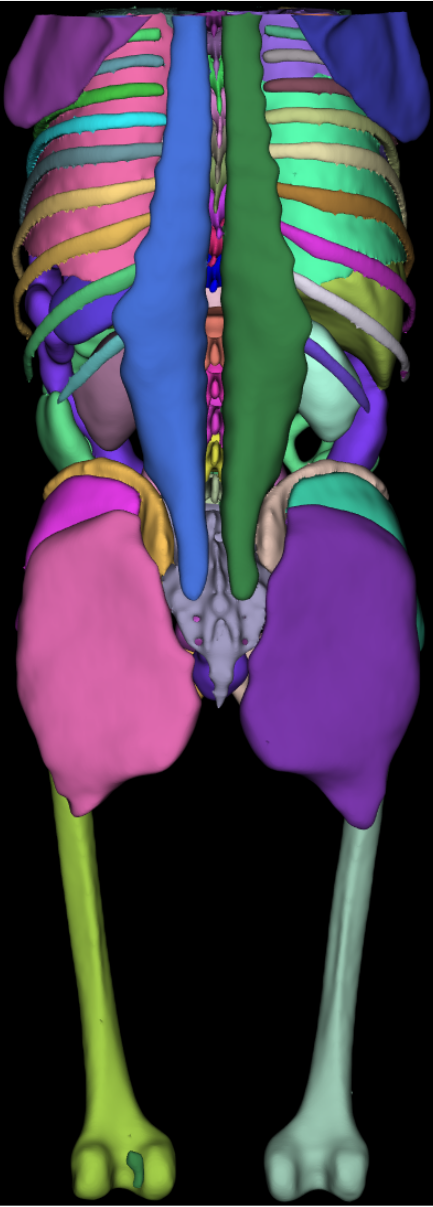
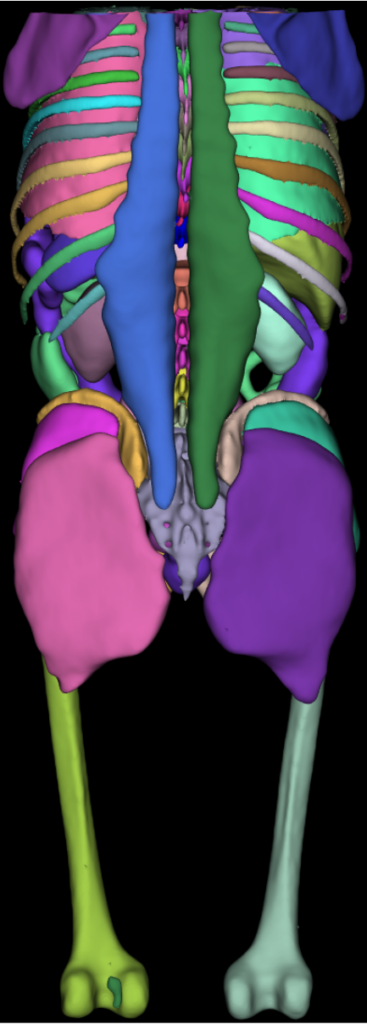
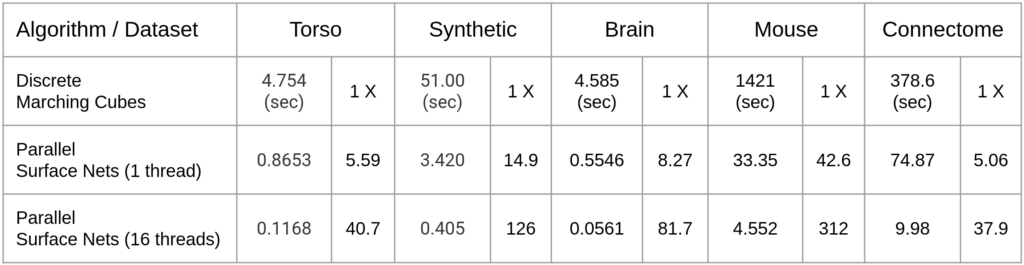
Surface Nets. The torso image shown in the introduction to this post was segmented by the AI-based TotalSegmentator. The dataset is a 317^2 by 835 slices volume, with 93 segmentation labels. The four-panel image shown below consists of a 1) synthetic dataset consisting of 128 random spheres (i.e., labeled regions) in a 512³ volume; 2) a segmented human brain of resolution 256³ with 313 labeled regions; 3) the Allen Mouse Brain Common Coordinate Framework (CCFv3) is a 3D reference space of an average mouse brain at 10um voxel resolution, created by serial two-photon tomography images of 1,675 young adult C57Bl6/J mice. The volume is of dimensions (1320 x 800 x 1140) with 688 labeled regions; and finally 4) 128 labels from a mouse brain connectomics dataset (the IARPA MICrONS Pinky100 segmented connectome of the visual cortex of a mouse produced with high-resolution electron microscopy, segmentation, and morphological reconstruction of cortical circuits). The connectome dataset is an extracted subvolume of dimensions 2048³ with 240 labels extracted. Timings below compare the speed of vtkSurfaceNets3D running on a 16-thread commodity laptop (Ubuntu, gcc 9.4.0 compiler, 64-gbyte memory) compared to vtkDiscreteMarchingCubes.

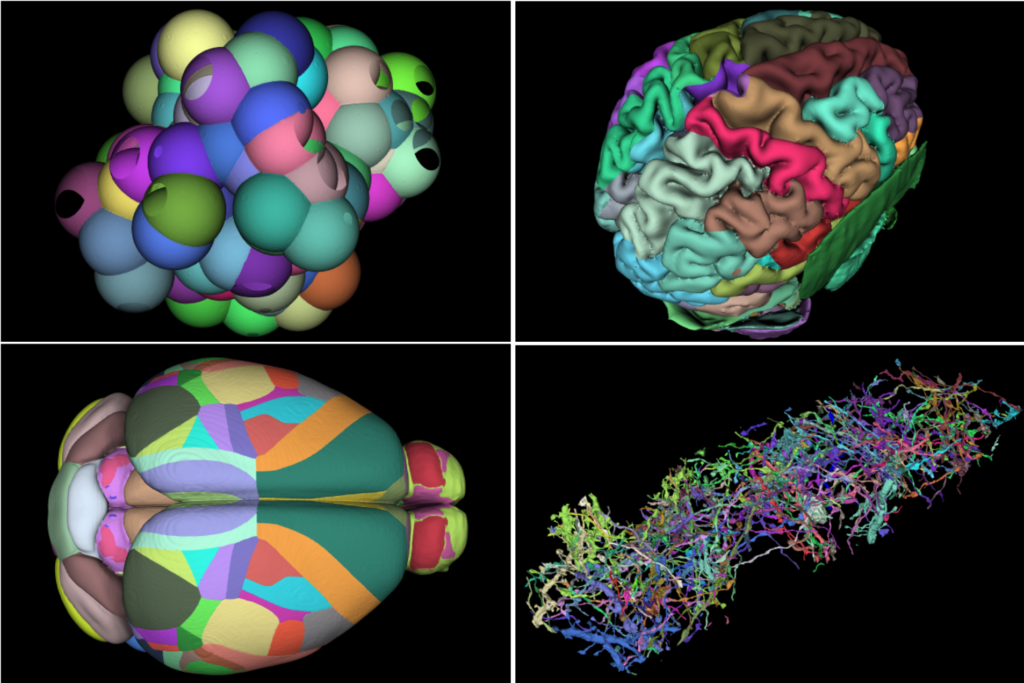
Execution time and speed up factors for these five datasets (i.e, the torso and four panel images above) are tabulated below with the maximum number of threads set to 16. Note that SurfaceNets is much faster than discrete Marching Cubes even when run sequentially.

What’s Next

In this day of web- and cloud-based computing, we are sometimes asked why we continue to focus so much effort on VTK’s C++ code base. While there are many compelling reasons including performance, data scale, and backward compatibility, this question it turns out is mostly irrelevant due to recent advances in computing system architectures, interoperability, and integration. Very large data is typically best treated using a client-server architecture, which by the way also fits well into a cloud computing environment. With new integration systems like trame, writing client-server applications is as straightforward as writing a desktop application. In addition, tools like Emscripten and Web Assembly enable C++ code to be easily converted into WASM blobs which can be readily incorporated into JavaScript web applications. And emerging graphics subsystems like WebGPU mean that web and C++ applications are interoperable across applications. The point is, with the emergence of new computing technologies, we can choose the best tools to write pieces of an application, and then readily deliver them to the desired computing environment.

One application area that we are particularly excited about is the creation of anatomical atlases, and interactive visual database systems that enable interactive exploration of data complex biology, providing graphical interfaces into underlying data. For example, it’s easy to imagine the rapid creation of personalized atlases enabling graphical access to associated medical records or other data. With AI systems now able to segment medical scans automatically and quickly, it’s possible to create customized, interactive access to personalized data. All that is needed are fast isocontouring algorithms to quickly construct and model geometry, which as described here are now readily available in VTK.

An area of ongoing research is the use of in-place decimation, remeshing, and/or sampling used to produce smaller, more compact output meshes. For example, using vtkSurfaceNets3D to extract thousands of segmented regions from a large volume can easily produce hundreds of millions of output triangles. One approach is to generate these isosurfaces, and then in a later pass, perform a reduction/decimation operation to reduce the mesh size. This of course means processing a lot of data most of which is discarded or transformed, a decidedly inefficient approach. Instead, methods that perform such operations as data is generated are likely be more efficient, and possibly even enable near-real time generation and rendering.